БСЭ - Большая Советская энциклопедия (Пр)

Преобразования функций. Существенное значение имеет также теория групп П. для теории аналитических функций. Там рассматриваются классы функций, не изменяющихся при П., образующих некоторую группу (см. Автоморфные функции ) .

Понятие П. играет важную роль и в функциональном анализе, где рассматриваются П. одного множества функций в другое. К таким П. относятся, например, Фурье преобразование , Лапласа преобразование и др. При этих П. каждой функции f ставится по определённому правилу в соответствие другая функция j. Например, преобразование Фурье имеет вид:

.

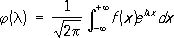Оно, как и преобразование Лапласа, относится к классу интегральных П., определяемых формулами вида:

.

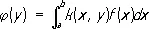В ряде случаев П. позволяют заменить операции над функциями более простыми операциями над их образами (например, дифференцирование — умножением на независимую переменную), что облегчает решение уравнений.

Многие уравнения можно записать в виде f = Af, где f — искомая функция, а А — символ П. В этом случае задача решения уравнения может быть истолкована как задача нахождения функции, не изменяющейся при П. Эта точка зрения, называемая принципом неподвижной точки, позволяет в ряде случаев устанавливать существование и единственность решения (см. Сжатых отображений принцип ) .

Лит.: Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971; Клейн Ф., Высшая геометрия, пер. с нем., М. — Л., 1939; его же, Элементарная математика с точки зрения высшей. Лекции..., пер. с нем., 2 изд., т. 2, М. — Л., 1934; Адамар Ж., Элементарная геометрия, пер. с франц., 4 изд., ч, 1, М., 1957.

Преобразова'ние представле'ния величины'в вычислительной технике, процесс перевода машинных переменные величин из аналоговой формы в цифровую (аналого-цифровое преобразование) или наоборот (цифро-аналоговое преобразование). П. п. в. связано, например, с необходимостью в процессе вычислений на ЦВМ вводить и выводить данные в аналоговой форме — при работе ЦВМ в системе автоматического регулирования технологическими процессами, при построении гибридных вычислительных систем и т.п. См. также Преобразователь функциональный .

Преобразова'тель функциона'льный, устройство, выходной сигнал которого у связан с одним либо несколько входными сигналами x i (где i = 1, 2,...) заданным алгоритмом функционирования. В зависимости от числа входных величин различают П. ф. одной, двух и более переменных. Функциональная зависимость выходных сигналов П. ф. от входных (единственного выходного при одном входном или каждого выходного при наличии нескольких входных сигналов) может быть задана в виде таблиц, графиков, аналитических выражений. Динамическая характеристика П. ф. y ( x 1, x 2,..., x n, t ) описывается дифференциальным уравнением, в правой части которого участвуют входной сигнал и его производные по времени (в общем случае), а в левой части — выходной сигнал и его производные по времени (в общем случае). Для инженерных расчётов динамическую характеристику П. ф. обычно удобнее всего характеризовать передаточными функциями по соответствующим каналам (входным сигналам).

По виду алгоритма функционирования в пределах предполагаемой рабочей области применения П. ф. делятся на линейные (в которых функциональная зависимость описывается с достаточным приближением прямой) и нелинейные (у которых функциональная зависимость криволинейная), в том числе кусочно-линейные. В зависимости от физической природы входных и выходных сигналов различают механические, электрические, пневматические, гидравлические и смешанные, в том числе электромеханические, электрогидравлические, пневмоэлектрические П. ф. По характеру представления исходных величин различают аналоговые, цифровые и гибридные П. ф. В гибридных П. ф. одновременно используется цифровое и аналоговое представление величин. При этом обычно входной сигнал делят на две части: одна представляется в аналоговой форме, а другая — в цифровой. Поэтому в состав таких П. ф. вводят цифро-аналоговые и аналого-цифровые преобразователи.

Самыми распространёнными и важными являются П. ф. одной входной величины, которые подразделяются в зависимости от алгоритма функционирования на динамические и формирующие. В динамических П. ф. осуществляется изменение входного сигнала во времени, например интегрирование, дифференцирование, временная задержка и т.п. В формирующем П. ф. входной сигнал изменяется по масштабу (например, в пропорциональных П. ф.) или форме воздействия, например при преобразовании непрерывного сигнала в дискретный (в импульсных, модуляционных, кодирующих П. ф.) либо наоборот — дискретного сигнала в непрерывный (в дискретно-аналоговых П. ф.).

В П. ф. осуществляются как простые, так и сложные преобразования. При простых преобразованиях выходная величина физически неотделима от входной, как, например, при преобразовании температуры в термоэдс или температуры в активное сопротивление. В сложных преобразованиях имеется не менее двух простых. Например, при преобразовании активного сопротивления в силу притяжения электромагнита имеется два простых преобразования: «активное сопротивление — магнитный поток» и «магнитный поток — сила притяжения сердечника».

Важнейшая характеристика П. ф. — погрешности при преобразовании, которые могут быть случайными и систематическими. Случайные погрешности обычно имеют нормальный закон распределения, и при нескольких последовательных преобразованиях общая погрешность равна D общ 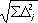, где D i— погрешности отдельных преобразований. Систематические погрешности преобразований складываются алгебраически (с учётом знаков). Не менее важная характеристика — чувствительность П. ф., т. е. отношение весьма малого изменения выходного сигнала к вызвавшему его также малому изменению входного сигнала. Для изменения чувствительности П. ф. вводится обратная связь (соответственно этому различают П. ф. с разомкнутой и замкнутой цепью воздействия).

П. ф. применяются в системах автоматического управления и регулирования, в аналоговых и гибридных вычислительных машинах, в устройствах кодирования (декодирования), в телемеханических системах, измерительных устройствах и т.п.

Лит.: Основы автоматического управления, 3 изд., М., 1974.