БСЭ БСЭ - Большая Советская Энциклопедия (БЕ)

Лит.: Попова О. С., Н. И. Бессарабова, М., 1960.

Н. И. Бессарабова. Кувшин. Фарфор. Подглазурная роспись кобальтом. Кон. 1940-х — нач. 1950-х гг. Музей народного искусства. Москва.

Бе'сселев год(назван по имени Ф. Бесселя ) , тропический год, за начало которого принимают момент времени, когда средняя долгота Солнца, уменьшенная на постоянный коэффициент аберрации (20,496''), в точности равна 280°. Начало Б. г. приходится на один и тот же момент времени для любого пункта Земли. Продолжительность Б. г. равна продолжительности тропического и в сутках может быть выражена формулой T 0= 365,24219879 — 0,00000614 Т , где Т — число столетий, прошедших с 1900.

Бе'ссель(Bessel) Фридрих Вильгельм (22.7.1784, Минден, — 17.3.1846, Кенигсберг), немецкий астроном, член Берлинской АН (1812). Двадцати лет вычислил орбиту кометы Галлея. В 1806 получил место ассистента в частной обсерватории в Лилиентале. Здесь Б. заново обработал данные наблюдений Дж. Брадлея, из которых определил постоянные рефракции, прецессии и нутации, по точности превзошедшие все прежние определения. В 1810 стал профессором Кёнигсбергского университета и построил здесь обсерваторию, директором которой оставался до самой смерти. На меридианном круге этой обсерватории Б. произвёл наблюдения 75011 звёзд между +47° и —16° склонения. Б. разработал теорию ошибок астрономических инструментов, открыл личное уравнение, т. е. систематическую ошибку, присущую данному наблюдателю. При обработке наблюдений Б. применял теорию вероятностей и способ наименьших квадратов. В 1838 при помощи гелиометра определил параллакс звезды 61 Лебедя, измерив т. о. расстояние до неподвижных звёзд. Разработал теорию солнечных затмений, определил массы планет и элементы спутников Сатурна. Большое значение имеют также работы Б. в области геодезии. В частности, совместно с И. Байером произвёл триангуляцию в Восточной Пруссии и на основании десяти лучших градусных измерений определил элементы земного сфероида. Им был изобретён базисный прибор .

В математике имя Б. носят т. н. цилиндрические функции 1-го рода (см. Бесселя функции ) и дифференциальное уравнение, которому они удовлетворяют (см. Бесселя уравнение ) , неравенство для коэффициентов ряда Фурье (см. Бесселя неравенство ) , а также одна из интерполяционных формул.

Соч.: Abhandlungen..., Bd 1—3, Lpz., 1875—76: в рус. пер. — Популярные чтения о научных предметах, М., 1859.

Лит.: Кларк А., Общедоступная история астрономии в XIX столетии, пер. с англ., Одесса, 1913.

Ф. В. Бессель.

Бе'сселя нера'венство,неравенство для коэффициентов ряда Фурье (см. Фурье ряд ) по произвольной ортонормированной системе функций j k ( x ) ( k = 1 , 2...), т. е. системе, определённой на некотором отрезке [ а, b ] и удовлетворяющей условиям ( k ¹ l )

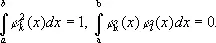
Если функция f ( x ) измерима на отрезке [ а, b ], а функция f 2( x ) интегрируема на этом отрезке и

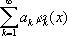
— ряд Фурье f ( x ) по системе j k( x ) , то справедливо Б. н.

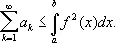
Б. н. играет важную роль во всех исследованиях, относящихся к теории ортогональных рядов. В частности, оно показывает, что коэффициенты Фурье функции f ( x ) стремятся к нулю при n ® ¥. Для тригонометрической системы функций это неравенство было получено Ф. Бесселем (1828). Если система функций j kтакова, что для любой функции f Б. н. обращается в равенство, то оно называется Парсеваля равенством .

С. Б. Стечкин.

Бе'сселя уравнение,линейное дифференциальное уравнение 2-го порядка вида

x 2 y ’’ + xy ’ + ( x 2- p 2) y = 0,

где параметр («индекс») р может принимать произвольные (комплексные) значения (названо по имени Ф. Бесселя ) . К этому уравнению приводят многочисленные физические задачи. Решения Б. у. называются цилиндрическими функциями ; о специальном классе цилиндрических функций см. статью Бесселя функции .

П. И. Лизоркин.

Бе'сселя функции, цилиндрические функции 1-го рода; возникают при рассмотрении физических процессов (теплопроводности, диффузии, колебаний и пр.) в областях с круговой и цилиндрической симметрией; являются решениями Бесселя уравнения.

Б. ф. J pпорядка (индекса) р, — ¥ < p < ¥, представляется рядом

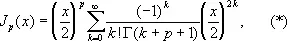
сходящимся при всех х. Её график при х > 0 имеет вид затухающего колебания; J p( x ) имеет бесчисленное множество нулей; поведение J p( x ) при малых | х | даётся первым слагаемым ряда (*), при больших х > 0 справедливо асимптотическое представление

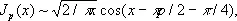
в котором отчётливо проявляется колебательный характер функции. Б. ф. «полуцелого» порядка р = n + 1/ 2выражаются через элементарные функции; в частности,

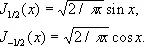
Б. ф. J p(m p n x/l ) (где m p n— положительные нули J p( x ) , р > - 1/ 2) образуют ортогональную с весом х в промежутке (0, l ) систему (см. Ортогональная система функций ) .

Функция J 0была впервые рассмотрена Д. Бернулли в работе, посвященной колебанию тяжёлых цепей (1732). Л. Эйлер, рассматривая задачу о колебаниях круглой мембраны (1738), пришёл к уравнению Бесселя с целыми значениями р = n и нашёл выражение J„ ( x ) в виде ряда по степеням х. В последующих работах он распространил это выражение на случай произвольных значений р. Ф. Бессель исследовал (1824) функции J p ( x ) в связи с изучением движения планет вокруг Солнца. Он составил первые таблицы для J 0( x ) , J 1( x ) , J 2( x ) .