БСЭ БСЭ - Большая Советская Энциклопедия (ВЕ)

Лит.: Арлей Н., Бух К. P., Введение в теорию вероятностей и математическую статистику, пер. с англ., М., 1951; Dixon W. J., Massey F. J., Introduction to statistical analysis, N. Y. — Toronto — L., 1957.

А. В. Прохоров.

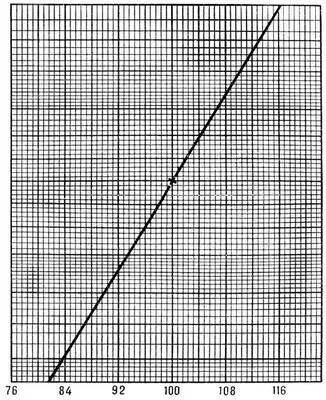
Образец вероятностной бумаги. Проведённая линия — график функции нормального распределения со средним 100 и стандартным отклонением 8.

Вероя'тностная ло'гика,логическая система, в которой высказываниям (суждениям, утверждениям, предложениям), помимо истины и лжи, приписываются «промежуточные» истинностные значения, называемые вероятностями истинности высказываний, степенями их правдоподобия, степенями подтверждения и т.п. Поскольку понятие вероятности естественно соотносить некоторым событиям, а наступление или не наступление события есть факт, допускающий (хотя бы в принципе) эмпирическую проверку (в широком смысле — включая так называемый мысленный эксперимент, а также вывод из знания о наступлении или не наступлении др. событий), то В. л. представляет собой уточнение индуктивной логики. Взаимные переходы от языка высказываний к языку событий и обратно совершаются настолько естественно, что выглядят почти тривиальными: каждому событию сопоставляется высказывание о его наступлении, а высказыванию сопоставляется событие, состоящее в том, что оно оказалось истинным. Специфика В. л. (даже полностью формализованной в логико-математических терминах) состоит в принципиальной неустранимости неполной достоверности («относительной истинности») посылок и выводов, присущей всякому индуктивному познанию.

Проблематика В. л. развивалась уже по существу в древности (например, Аристотелем), а в новое время — Г. В. Лейбницем, Дж. Булем, У. С. Джевонсом, Дж. Венном.

Как логическая система, В. л. — разновидность многозначной логики: истинным высказываниям (достоверным событиям) приписывается истинностное значение (вероятность) 1, ложным высказываниям (невозможным событиям) — значение 0; гипотетическим же высказываниям может приписываться в качестве значения любое действительное число из интервала (0, 1). Вероятность гипотезы, зависящая как от её содержания (формулировки), так и от информации об уже имеющемся знании («опыта»), есть их функция. Над истинностными значениями (вероятностями) гипотез определяются логические операции: конъюнкция (соответствующая умножению событий в теории вероятностей) и дизъюнкция (соответствующая сложению событий); мерой (значением) отрицания гипотезы является вероятность события, состоящего в её неподтверждении. Значения гипотез образуют при этом так называемую нормированную булеву алгебру, сравнительно простой и хорошо разработанный аппарат которой позволяет легко аксиоматизировать теорию вероятностей и является простейшим вариантом В. л.

В соответствии с др. трактовкой понятия вероятности, связанной с так называемой частотной концепцией (определением) вероятности (А. Пуанкаре, М. Смолуховский, Р. Мизес ) , в В. л. получили развитие идеи, согласно которым основным объектом её рассмотрения являются не вероятности отдельных событий, а случайные процессы, реализуемые в простейшем случае в виде случайных двоичных последовательностей, то есть последовательностей нулей и единиц (соответствующих единичным актам не наступления и наступления некоторого события при повторных испытаниях).

Интенсивно развивается и проблематика В. л., возникающая при сопоставлении обоих упомянутых подходов (Р. Карнап, Б. Рассел и др.), а также базирующаяся на связи теоретико-вероятностных понятий с идеями теории информации и логической семантики. Все эти направления находятся в процессе разработки как по линии усовершенствования собственно математического аппарата В. л., так и в отношении теоретико-познавательной интерпретации возникающих систем (причём именно в последней области и сосредоточены главные трудности В. л.).

Лит. см. при статьях Вероятностей теория, Индуктивная логика, Многозначная логика.

Ю. А. Гастев.

Вероя'тностный автома'т,система, в которой переход из одного состояния в другое происходит случайным образом. Вероятность этого перехода определяется последовательностью его предыдущих состояний ( a 1, a 2,..., a i ,..., a n ) и входными сигналами ( S 1, S 2,..., S m ) и записывается в виде функции Р ( a i ® a j, S k ) , где a i ® a j означает переход из состояния ( a i в состояние a j).

В. а. используются в формальных моделях процессов обучения, в моделях сложного поведения, когда реакция автомата неоднозначна.

Примером В. а. может служить система автоматического управления движением транспорта на перекрёстке двух улиц с разной интенсивностью движения. Для простоты рассмотрим В. а. с двумя состояниями: «откр» — проезд по магистрали (улица с интенсивным движением) открыт и «закр» — магистраль перекрыта, разрешено поперечное движение. Входных сигналов тоже два: S 1 — «на поперечной улице ждет транспорт» и S 2— «эта улица пуста». Переходные вероятности определены так:

Р (закр ® закр, S 2) = Р (откр ® закр, S 2) = 0;

Р (откр ® откр, S 2) = Р (закр ® откр, S 2) = 1;

Р (откр ® откр, S 1 ) = 0,7;

Р (откр ® закр, S 1 ) = 0,3;

Р (закр ® закр, S 1 ) = 0,5;

Р (закр ® откр, S 1 ) = 0,5.

Такой автомат по мере надобности пропускает поперечный транспорт, но не перекрывает магистраль при появлении на поперечном направлении каждой отдельной машины. Численные значения вероятностей переходов и время основного такта работы автомата необходимо выбирать исходя из конкретного транспортного режима.

В. а. можно представить в виде системы, состоящей из детерминированного автомата и случайных чисел датчика, подающего на один из входов автомата независимые сигналы с заданным распределением вероятностей.

Ю. А. Шрейдер.

Вероя'тностный проце'сс,то же, что случайный процесс.

Вероя'тностьматематическая, числовая характеристика степени возможности появления какого-либо определённого события в тех или иных определённых, могущих повторяться неограниченное число раз условиях. Как категория научного познания понятие «В.» отражает особый тип связей между явлениями, характерных для массовых процессов. Категория В. лежит в основе особого класса закономерностей — вероятностных или статистических закономерностей.