БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

Профилактика: строгое соблюдение рационального вскармливания, режима питания и ухода.

Лит.: Маслов М. С., Лекции по факультетской педиатрии, ч. 1, Л., 1963, с. 18—43.

Р. Н. Рылеева, М. Я. Студеникин.

Дисперги'рование(от лат. dispergo — рассеиваю, рассыпаю), тонкое измельчение твёрдых тел и жидкостей в окружающей среде, приводящее к образованию дисперсных систем ; порошков, суспензий, эмульсий. Д. жидкостей в газах (воздухе) обычно называется распылением, а в жидкостях — эмульгированием. Д. требует затраты работы тем большей, чем выше требуемая степень измельчения и поверхностная энергия на границе измельчаемого тела с окружающей средой. В промышленности Д. твёрдых тел производят с помощью мельниц различной конструкции (шаровых, вибрационных, коллоидных, струйных и др.), звуковых и ультразвуковых вибраторов. При Д. жидкостей применяют также турбулентное (вихревое) перемешивание, различного рода гомогенизаторы — аппараты для получения однородных эмульсий. В лабораториях и аптеках для Д. широко используют ступы.

Механическим Д. получают дисперсии с размером частиц до 10—1 мкм . Высокоэффективное измельчение возможно лишь в присутствии диспергаторов и эмульгаторов — поверхностно-активных веществ , снижающих поверхностную энергию диспергируемых твёрдых тел или жидкостей и работу Д. (см. также Ребиндера эффект ). Кроме того, они препятствуют агрегации, т. е. слипанию мелких частиц и слиянию капель ( коагуляции и коалесценции ). В случае очень сильного понижения поверхностной энергии может иметь место самопроизвольное Д. без затраты внешней работы — под влиянием теплового движения (см. Лиофильные и лиофобные коллоиды ).

Д. применяют при получении цементов, пигментов, наполнителей, муки, многих пищевых продуктов и кормовых концентратов, при использовании с.-х. ядохимикатов ( пестицидов ), при сжигании жидкого и твёрдого топлива и во многих других технологических процессах.

Лит.: Ходаков Г. С., Физика измельчения, М., [в печати]; его же, Тонкое измельчение строительных материалов, М., [в печати]; Гийо Р., Проблема измельчения и её развитие, пер. с франц., М., 1964.

Дисперсио'нная среда',непрерывная фаза (тело), в объёме которой распределена другая (дисперсная) фаза в виде мелких твёрдых частиц, капелек жидкости или пузырьков газа. Д. с. может быть твёрдой, жидкой или газовой; в совокупности с дисперсной фазой она образует дисперсные системы . См. также Коллоидные системы .

Дисперсио'нно-тверде'ющие спла'вы,материалы, упрочнённые дисперсными частицами избыточной фазы, выделяющимися в процессе старения. См. Дисперсно-упрочненные материалы , Старение металлов .

Дисперсио'нные при'змы,призмы для пространственного разделения излучений различных длин волн; применяются главным образом в спектральных приборах . Разделение излучений в Д. п. является результатом зависимости угла отклонения d луча, прошедшего через призму (см. рис. ), от показателя преломления n , различного для лучей разных длин волн l (см. Дисперсия света ). Качество Д. п. характеризуется угловой дисперсией Dd/Dl, которая зависит от материала призмы (величин n и D n /Dl), преломляющего угла a и угла падения i 1:

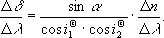
В зависимости от исследуемой области спектра применяются Д. п. из различных материалов: стекла (флинта) — для видимой области; кристаллического кварца, флюорита и др. — для ультрафиолетовой; фтористого лития, каменной соли и др. — для инфракрасной.

Лит.: Ландсберг Г. С., Оптика, 4 изд., М. — Л., 1957 (Общий курс физики, т. 3).

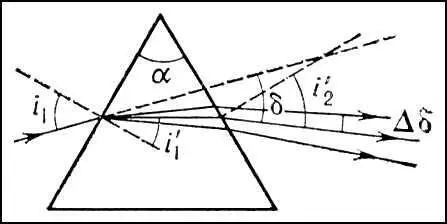
Рис. к ст. Дисперсионные призмы.

Дисперсио'нный ана'лизв математике, статистический метод выявления влияния отдельных факторов на результат эксперимента. Первоначально Д. а. был предложен английским статистиком Р. Фишером (1925) для обработки результатов агрономических опытов по выявлению условий, при которых испытываемый сорт с.-х. культуры даёт максимальный урожай. Современные приложения Д. а. охватывают широкий круг задач экономики, биологии и техники и трактуются обычно в терминах статистической теории выявления систематических различий между результатами непосредственных измерений, выполненных при тех или иных меняющихся условиях. Если значения неизвестных постоянных a 1 ,...., a n могут быть измерены с помощью различных методов или измерительных средств M 1 ,..., М m и в каждом случае систематическая ошибка может зависеть как от выбранного метода, так и от неизвестного измеряемого значения a i , то результаты измерений x ij представляют собой суммы вида

x ij = a i , + b ij + d ij ,

i = 1, 2,..., n ; j = 1, 2,..., m ,

где b ij — систематическая ошибка, возникающая при измерении a i по методу M j , d ij — случайная ошибка. Такая модель называется двухфакторной схемой Д. а. (первый фактор — измеряемая величина, второй — метод измерения). Дисперсии эмпирических распределений, соответствующих множествам случайных величин

x ij , x ij - x i *- x * j + x **, x i *и x * j , где

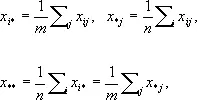
выражаются формулами:

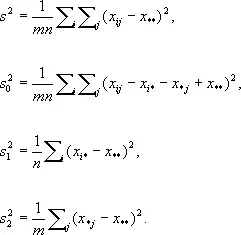
Эти дисперсии удовлетворяют тождеству

s 2 = s 2 0 + s 2 1 + s 2 2 ,

которое и объясняет происхождение названия Д. а.

Если величины систематических ошибок не зависят от метода измерений (т. е. между методами измерений нет систематических расхождений), то отношение s 2 2/s 2 0 близко к единице. Это свойство лежит в основе критерия для статистического выявления систематических расхождений: если s 2 2ls 2 0 значимо отличается от единицы, то гипотеза об отсутствии систематических расхождений отвергается. Значимость отличия определяется в согласии с законом распределения вероятностей случайных ошибок измерений. В частности, если все измерения равноточны и случайные ошибки подчиняются нормальному распределению, то критические значения для отношения s 2 2/s 2 0 определяются с помощью таблиц так называемого F -распределения (распределения дисперсионного отношения).