БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

Приближённая теория Д. с. основана на применении Гюйгенса- Френеля принципа . Для качественного рассмотрения простейших случаев Д. с. может быть применено построение зон Френеля . При прохождении света от точечного источника через небольшое круглое отверстие в непрозрачном экране или вокруг круглого непрозрачного экрана наблюдаются дифракционные полосы в виде концентрических окружностей. Если отверстие оставляет открытым чётное число зон, то в центре дифракционной картины получается тёмное пятнышко, при нечётном числе зон — светлое. В центре тени от круглого экрана, закрывающего не слишком большое число зон Френеля, получается светлое пятнышко.

Различают 2 случая Д. с. — дифракция сферической волны, при которой размер отверстия сравним с размером зоны Френеля, т. е.

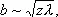
где b — размер отверстия, z — расстояние точки наблюдения от экрана, l — длина волны (дифракция Френеля), и Д. с. в параллельных лучах, при которой отверстие много меньше одной зоны Френеля, т. е.

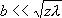
(дифракция Фраунгофера). В последнем случае при падении параллельного пучка света на отверстие пучок становится расходящимся с углом расходимости j ~ l/ b (дифракционная расходимость).

Большое практическое значение имеет случай Д. с. на щели. При освещении щели параллельным пучком монохроматического света на экране получается ряд тёмных и светлых полос, быстро убывающих по интенсивности. Если свет падает перпендикулярно к плоскости щели, то полосы расположены симметрично относительно центральной полосы ( рис. 2 ), а освещённость меняется вдоль экрана периодически с изменением j, обращаясь в нуль при углах j, для которых sin j = m /l b ( m = 1, 2, 3 ....). При промежуточных значениях освещённость достигает максимальных значений. Главный максимум имеет место при m = 0, при этом sin j = 0, т. е. j = 0. Следующие максимумы, значительно уступающие по величине главному, соответствуют значениям j, определённым из условий: sin j = 1,43 l/ b , 2,46 l/ b , 3,47 l/ b и т.д.

С уменьшением ширины щели центральная светлая полоса расширяется, а при данной ширине щели положение минимумов и максимумов зависит от l, т. е. расстояние между полосами тем больше, чем больше l. Поэтому в случае белого света имеет место совокупность соответствующих картин для разных цветов. При этом главный максимум будет общим для всех l и представится в виде белой полоски, переходящей в цветные полосы с чередованием цветов от фиолетового к красному.

Если имеются 2 идентичные параллельные щели, то они дают одинаковые накладывающиеся друг на друга дифракционные картины, вследствие чего максимумы соответственно усиливаются, а кроме того, происходит взаимная интерференция волн от первой и второй щелей, значительно осложняющая картину. В результате минимумы будут на прежних местах, т.к. это те направления, по которым ни одна из щелей не посылает света. Кроме того, возможны направления, в которых свет, посылаемый двумя щелями, взаимно уничтожается. Т. о., прежние минимумы определяются условиями: b sin j = l, 2l, 3l, ..., добавочные минимумы d sin j = l/2, 3l/2, 5l/2, ... ( d — размер щели b вместе с непрозрачным промежутком а ), главные максимумы d sin j = 0,l, 2l, 3l, ..., т. е. между двумя главными максимумами располагается один добавочный минимум, а максимумы становятся более узкими, чем при одной щели. Увеличение числа щелей делает это явление ещё более отчётливым (см. Дифракционная решётка ).

Д. с. играет существенную роль при рассеянии света в мутных средах, например на пылинках, капельках тумана и т.п. На Д. с. основано действие спектральных приборов с дифракционной решёткой (дифракционных спектрометров). Д. с. определяет предел разрешающей способности оптических приборов (телескопов, микроскопов и др.). Благодаря Д. с. изображение точечного источника (например, звезды в телескопе) имеет вид кружка с диаметром l flD , где D — диаметр объектива, а f — его фокусное расстояние. Расходимость излучения лазеров также определяется Д. с. Для уменьшения расходимости лазерного пучка его преобразуют в более широкий пучок при помощи телескопа, и тогда расходимость излучения определяется диаметром D объектива по формуле j ~ l/ D .

Лит.: Ландсберг Г. С., Оптика, 4 изд., М., 1957 (Общий курс физики, т. 3); Горелик Г. С., Колебания и волны, 2 изд., М., 1959, гл. 9.

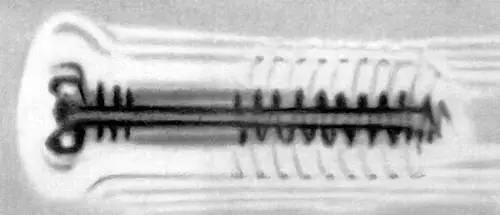
Рис. 1. Тень винта, окружённая дифракционными полосами.

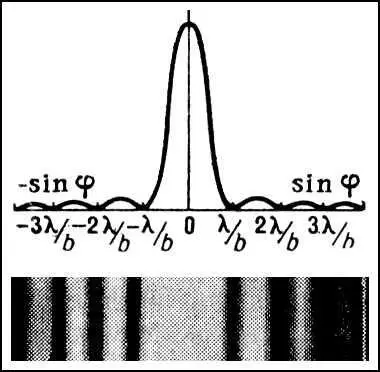
Рис. 2. Дифракция Фраунгофера на щели.

Дифра'кция части'ц,рассеяние микрочастиц (электронов, нейтронов, атомов и т.п.) кристаллами или молекулами жидкостей и газов, при котором из начального пучка частиц данного типа возникают дополнительно отклонённые пучки этих частиц; направление и интенсивность таких отклонённых пучков зависят от строения рассеивающего объекта.

Д. ч. может быть понята лишь на основе квантовой теории. Дифракция — явление волновое, оно наблюдается при распространении волн различной природы: дифракция света, звуковых волн, волн на поверхности жидкости и т.д. Дифракция при рассеянии частиц, с точки зрения классической физики, невозможна.

Квантовая механика устранила абсолютную грань между волной и частицей. Основным положением квантовой механики, описывающей поведение микрообъектов, является корпускулярно-волновой дуализм , т. е. двойственная природа микрочастиц. Так, поведение электронов в одних явлениях, например при наблюдении их движения в камере Вильсона или при измерении электрического заряда в фотоэффекте , может быть описано на основе представлений о частицах, в других же, особенно в явлениях дифракции, — только на основе представления о волнах. Идея «волн материи» была высказана французским физиком Л. де Бройлем в 1924 и вскоре получила блестящее подтверждение в опытах по Д. ч.

Согласно квантовой механике, свободное движение частицы с массой m и импульсом р = mv (где v — скорость частицы) можно представить как плоскую монохроматическую волну y 0( волну де Бройля ) с длиной волны

l = h/p , (1)

распространяющуюся в том же направлении (например, в направлении оси х ), в котором движется частица ( рис. 1 ). Здесь h — Планка постоянная . Зависимость y 0от координаты х даётся формулой