БСЭ БСЭ - Большая Советская Энциклопедия (ДВ)

Если компоненты А и В обладают неограниченной взаимной растворимостью как в жидком, так и в твёрдом состоянии, то из одной жидкой фазы L при охлаждении выпадает только одна кристаллическая фаза — твёрдый раствор S ( рис. 3 ). Диаграмма состояния такой Д. с. может быть без максимума и минимума ( рис. 3, I ), с максимумом ( рис. 3, II ) и с минимумом ( рис. 3, III ) . Изотермы свойств имеют вид непрерывных кривых, обращенных выпуклостью вверх ( рис. 3, IV ) или вниз ( рис. 3, V ).

Если взаимная растворимость А и В в жидком состоянии не ограничена, а в твёрдом — ограничена, то в случае образования эвтектики последняя состоит из смеси двух твёрдых растворов ( и b ( рис. 4 ), предельные концентрации которых отвечают точкам F и G при эвтектической температуре и точкам М и N при комнатной. Изотермы состав — свойство (отвечающие температуре t ) состоят из 3 ветвей e Am 1n 1e Bи eAm 2n 2e B , точки m 1, m 2и n 1, n 2отвечают предельным концентрациям твёрдых растворов a и b при температуре t.

В случае, когда из жидкости L кристаллизуется одно химическое соединение С, плавящееся без разложения, и твёрдые растворы отсутствуют, на кривой ликвидуса наблюдается либо рациональный максимум М, либо сингулярная точка D, отвечающие составу соединения С, и две эвтектические точки E 1 и E 2, отвечающие эвтектикам, образуемым С с А и В соответственно ( рис. 5 ). Изотермы свойств имеют вид двух прямых, пересекающихся на ординате соединения С. Более сложные случаи диаграмм состояния Д. с. см. в приведённой ниже литературе.

Лит.: Курнаков Н. С., Избр. труды, т. 1—3, М., 1960—63; Вол А. Е., Строение и свойства двойных металлических систем, т. 1—2, М., 1959—62; Хансен М., Андерко К., Структуры двойных сплавов, пер. с англ. , М. , 1962; см. также лит. при ст. Диаграмма состояния .

С. А. Погодин.

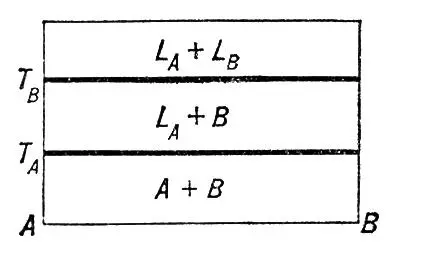
Рис. 1 к ст. Двойные системы.

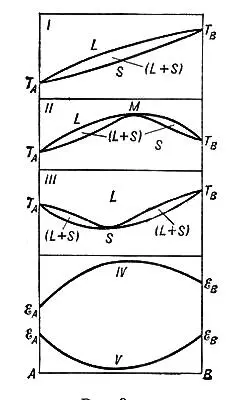
Рис. 3 к ст. Двойные системы.

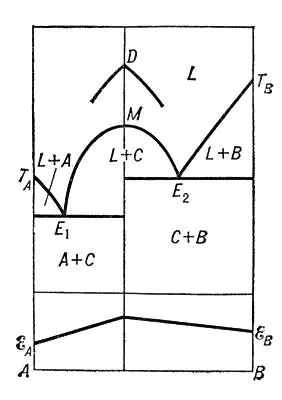
Рис. 5 к ст. Двойные системы.

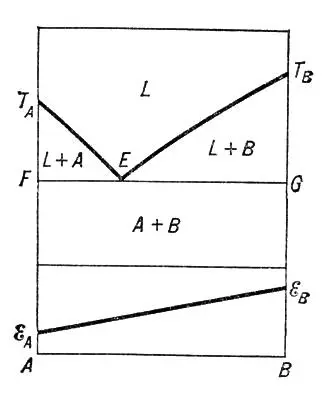
Рис. 2 к ст. Двойные системы.

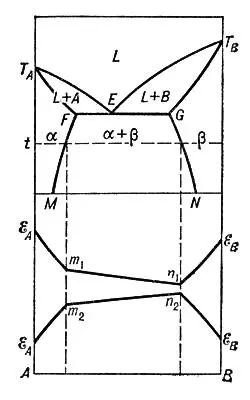
Рис. 4 к ст. Двойные системы.

Дво'йственная и'стина,двойная истина, термин, обозначающий учение о разделении философских и богословских истин, согласно которому истинное в философии может быть ложным в теологии и наоборот. Учение о Д. и. возникло в средние века, в эпоху распространения философии Аристотеля, когда обнаружилось, что ряд философских положений аристотелевской системы противоречит догматам ислама и христианства. Наиболее влиятельным мыслителем, опиравшимся на учение о Д. и. в своей полемике с мусульманскими богословами, был Ибн Рушд. Из этого же учения исходили и французский аверроизм 13 в. (его главой в Парижском университете был Сигер Брабантский), представители английского номинализма ( Иоанн Дунс Скот, У. Оккам ) . Широкое распространение учение о Д. и. получило в эпоху Возрождения (Помпонацци, падуанская школа аверроистов и др.). Учение о Д. и. способствовало развитию рационализма.

Дво'йственности при'нцип,принцип, формулируемый в некоторых разделах математики и заключающийся в том, что каждому верному утверждению этого раздела отвечает двойственное утверждение, которое может быть получено из первого путём замены входящих в него понятий на другие, т. н. двойственные им понятия.

1) Д. п. формулируется в проективной геометрии на плоскости. При этом двойственными понятиями являются, например, «точка» и «прямая», «точка лежит на прямой» и «прямая проходит через точку». Каждой аксиоме в проективной геометрии на плоскости формулируется двойственное предложение, которое может быть доказано с помощью этих же аксиом (этим обосновывается Д. п. в проективной геометрии на плоскости). Двойственными утверждениями в проективной геометрии на плоскости являются известные теоремы Паскаля и Брианшона. Первая из этих теорем утверждает, что во всяком шестивершиннике, вписанном в линию 2-го порядка, точки пересечения противоположных сторон лежат на одной прямой ( рис. 1 ). Вторая теорема утверждает, что во всяком шестистороннике, описанном около линии 2-го порядка, прямые, соединяющие противоположные вершины, пересекаются в одной точке ( рис. 2 ).

2) Д. п. в абстрактной теории множеств. Пусть дано множество М. Рассмотрим систему всех его подмножеств А, В, С и т.д. Справедливо следующее предложение: если верна теорема о подмножествах множества М, которая формулируется лишь в терминах операций суммы, пересечения и дополнения, то верна также и теорема, получающаяся на данной путём замены операции суммы и пересечения соответственно операциями пересечения и суммы, пустого множества L — всем множеством М, а множества М — пустым множеством L. При этом дополнение суммы заменяется пересечением дополнений, а дополнение пересечения — суммой дополнений.

Пример 1. Верному соотношению

( A È В ) Ç С = ( A Ç С ) È ( ВÇ С )

двойственно соотношение (также верное)

( АÇ B ) È C = ( A È С ) Ç ( В È С )

Пример 2. Верному соотношению

(AÈB)È(ĀÇ`B) = M

двойственно соотношение (также верное)

(ĀÇ `B)Ç(АÈ В) = L ,

где Ā , `B — дополнения множеств А, В во множестве М, А Ç В — сумма множеств А и В, A Ç В— их пересечение.

3) Д. п. имеет место в математической логике (в исчислении высказываний и в исчислении предикатов).

4) О топологических законах двойственности см. Топология.

Лит.: Ефимов Н. В., Высшая геометрия, 4 изд., М., 1961; Александров П. С., Введение в общую теорию множеств и функций, М. — Л., 1948; Гильберт Д. и Аккерман В., Основы теоретической логики, пер. с нем., М., 1947.

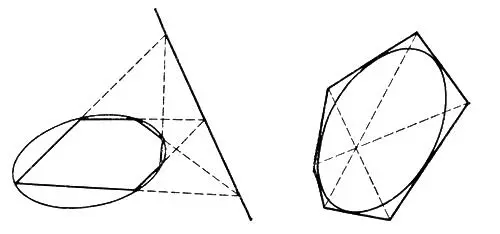
Рисунки 1 (слева) и 2 (справа) к ст. Двойственности принцип.

Дво'йственный тари'ф,см. в ст. Таможенные тарифы.