БСЭ БСЭ - Большая Советская Энциклопедия (ДВ)

составленное из элементов бесконечной матрицы || u mn || ( m, n = 1, 2, ...); эти элементы могут быть числами (тогда Д. р. называются числовым), функциями от одного или нескольких переменных (функциональный Д. р.) и т. д. Для Д. р. принята сокращённая запись

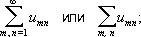
u mn называется общим членом Д. р.

Конечные суммы

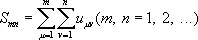
называются частичными суммами Д. р. Если существует предел

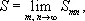
когда m и n независимо друг от друга стремятся к бесконечности, то этот предел называется суммой Д. р. и Д. р. называются сходящимся. Теория сходимости Д. р. значительно сложнее соответствующей теории для простых рядов; например, в отличие от простых рядов, из сходимости Д. р. не вытекает, что его частичные суммы ограничены.

Выражение

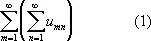
называется повторным рядом. Его надо понимать в том смысле, что сначала вычисляются суммы

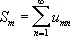
всех внутренних рядов, а затем рассматривается ряд

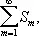
составленный из этих сумм. Если повторный ряд (1) сходится и имеет сумму S, то её называют суммой Д. р. по строкам. Аналогично определяется сумма S' Д. р. по столбцам. Из сходимости Д. р. не вытекает, что сходятся внутренние Ряды

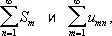
так что суммы по строкам и по столбцам могут и не существовать. Напротив, если Д. р. расходится, то может оказаться, что существуют суммы по строкам и по столбцам и S ¹ S'. Однако, если Д. р. сходится и имеет сумму S и существуют суммы по строкам и по столбцам, то каждая из этих сумм равна S . Это обстоятельство постоянно используется при фактическом вычислении суммы Д. р.

Наиболее важными классами Д. р. являются двойные степенные ряды, двойные ряды Фурье и квадратичные формы с бесконечным числом переменных. Для Д. р. Фурье

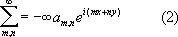
одним из стандартных пониманий суммы таких рядов является следующее: образуются круговые (или сферические) частичные суммы

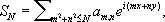
где суммирование распространяется на всевозможные пары целых чисел ( m, n ) , для которых m 2+ n 2 < N, и рассматривается предел 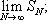этот предел называется сферической суммой Д. р. Фурье (2). Многие важные функции изображаются с помощью Д. р., например эллиптическая функция Вейерштрасса.

Кратный ряд (точнее, s-кpaтный ряд) есть выражение вида

S m, n, …, pu mn … q,

составленное из членов таблицы || u mn...p ||. Каждый член этой таблицы занумерован s индексами m , n , ..., р, и эти индексы пробегают независимо друг от друга все натуральные числа. Теория кратных рядов совершенно аналогична теории Д. р.

Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 6 изд., т. 2, М., 1966.

С. Б. Стечкин.

Двойно'й суперфосфа'т, концентрированное фосфорное удобрение; см. Суперфосфат.

Двойно'й электри'ческий сло'й,два весьма близких друг к другу слоя электрических зарядов разного знака, но с одинаковой поверхностной плотностью, возникающие на границе раздела двух фаз. Д. э. с. в целом электронейтрален. При пересечении Д. э. с. электрический потенциал изменяется скачком. Д. э. с. на поверхности металла возникает из-за того, что электроны металла несколько выходят за пределы решётки, образованной положительными ионами. Скачок потенциала в таком Д. э. с. является составной частью работы выхода электрона из металла.

Для электрохимии большое значение имеет Д. э. с. на границе раздела металл — электролит. При погружении металла в раствор, содержащий ионы этого металла, образуется специфический для границы электрод — раствор ионный Д. э. с. дополнительно к Д.э.с., существовавшему на поверхности металла до погружения, и Д. э. с., возникающему в результате ориентации полярных молекул растворителя (например, воды) у поверхности металла. Так, при погружении серебряной пластинки в раствор KNO 3, содержащий очень мало AgNO 3, ионы Ag+ переходят из металла в раствор, избыточные электроны в металле заряжают его поверхность отрицательно и притягивают из раствора ионы К +, образующие у поверхности вторую (положительную) обкладку Д. э. с. (см. рис. ). Возникающий скачок потенциала приостанавливает дальнейший переход ионов Ag+, и наступает равновесие электрода с раствором. Если концентрация AgNO 3в растворе велика, то, наоборот, ионы Ag+ из раствора переходят в металл, его поверхность заряжается положительно и притягивает из раствора ионы NO 3Существует промежуточная концентрация ионов металла, при которой поверхность металла не заряжается; соответствующий потенциал электрода называется потенциалом нулевого заряда, или нулевой точкой. Важное понятие о нулевой точке как величине, характерной для данного электрода, введено в электрохимию советским учёным А. Н. Фрумкиным.

На ноны в Д. э. с. действуют одновременно электростатические силы и силы теплового движения. В результате взаимно противоположного влияния этих сил лишь часть ионов остаётся непосредственно вблизи поверхности электрода (плотная часть Д. э. с., или слой Гельмгольца), а остальные распределяются диффузно в растворе на некотором расстоянии от электрода (диффузный Д. э. с., или слой Гуи). Степень диффузности увеличивается с ростом температуры, а также при уменьшении концентрации раствора электролита и при уменьшении заряда электрода. Средняя толщина плотной части Д. э. с. порядка радиуса иона (несколько А), поэтому Д. э. с. обладает высокой электрической ёмкостью (~10 -5 ф/см 2 ) и внутри него действует сильное электрическое поле (~10 6 в/см ) .

Строение Д. э. с. оказывает большое влияние на электрические свойства межфазных границ и на протекающие на них процессы — прежде всего, на механизм и кинетику электрохимических реакций, на электрокинетические явления, на устойчивость коллоидных систем и т. п. Для исследования Д. э. с. используются методы измерения поверхностного натяжения и ёмкости, адсорбционные измерения и др.