БСЭ БСЭ - Большая Советская Энциклопедия (КИ)

При изучении сложного движения точки её движение, а также скорость и ускорение по отношению к основной системе отсчёта называют условно абсолютными, а по отношению к подвижной системе — относительными. Движение самой подвижной системы отсчёта и всех неизменно связанных с ней точек пространства по отношению к основной системе называют переносным движением, а скорость и ускорение той точки подвижной системы отсчёта, с которой в данный момент совпадает движущаяся точка, называют переносной скоростью и переносным ускорением. Например, если основную систему отсчета связать с берегом, а подвижную с пароходом, идущим по реке, и рассмотреть качение шарика по палубе парохода (считая шарик точкой), то скорость и ускорение шарика по отношению к палубе будут относительными, а по отношению к берегу — абсолютными; скорость же и ускорение той точки палубы, которой в данный момент касается шарик, будут для него переносными. Аналогичная терминология используется и при изучении сложного движения твёрдого тела.

Основные задачи К. сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, т. е.

n a= n oтн+ n пер,

а абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и поворотного, или кориолисова (см. Кориолиса ускорение ) , т. е.

w a= w oтн+w пер+w kop.

Для твердого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений (см. Винтовое движение ) .

В К. непрерывной среды устанавливаются способы задания движения этой среды, рассматривается общая теория деформаций и определяются так называемые уравнения неразрывности, отражающие условия непрерывности среды.

Лит. см. при ст. Механика.

С. М. Тарг.

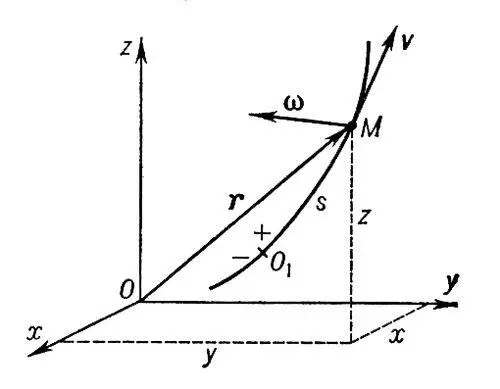
Рис. 1 к ст. Кинематика.

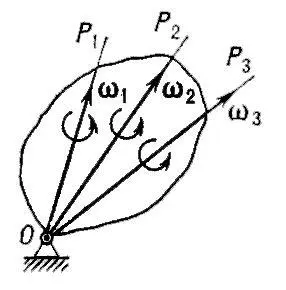
Рис. 4 к ст. Кинематика.

Рис. 2 к ст. Кинематика.

Рис. 3 к ст. Кинематика.

Кинема'тика звёздных систе'м,раздел звёздной астрономии; то же, что звёздная кинематика.

Кинема'тика механи'змов,раздел теории машин и механизмов, в котором изучают геометрическую сторону движения частей (звеньев) механизма, пренебрегая вызывающими его причинами. Исследования К. м. основываются на положении о том, что любой механизм состоит из подвижно соединённых твёрдых тел — звеньев, движения которых определяются движением одного или нескольких звеньев, называемых ведущими.

К. м. решает задачи кинематического анализа и кинематического синтеза (см. Синтез механизмов ) . Основные задачи кинематического анализа: определение положений звеньев, траекторий отдельных точек механизма, угловых скоростей и ускорений звеньев, линейных скоростей и ускорений отдельных точек механизма. Для решения каждой из этих задач должны быть заданы постоянные геометрические параметры механизма, определяющие его кинематические свойства и законы движения ведущих звеньев. Например, для плоского шарнирного механизма ( рис. 1 ) должны быть известны расстояния между центрами шарниров и закон движения ведущего звена АВ. Для кулачкового механизма ( рис. 2 ) должны быть заданы профиль кулачка 1 и закон его движения, радиус ролика 3, расстояния между центрами шарниров С и D, А и D. Положения звеньев определяют графическими и аналитическими методами.

Более простые графические методы заключаются в следующем. Если для механизма ( рис. 1 ) известно положение звена АВ и расстояния между центрами шарниров, можно положения всех остальных звеньев определить засечками циркуля. Таким образом, задача для плоских механизмов всегда может быть сведена к определению точек пересечения плоских кривых. Графические построения для пространственных механизмов усложняются, т.к. они связаны с определением линий и точек пересечения пространственных фигур. Однако в пределах точности графических построений всегда можно построить положения всех звеньев плоских и пространственных механизмов любой сложности.

Аналитические методы позволяют определять положения звеньев с заранее заданной точностью. Задача сводится к решению системы нелинейных уравнений. Для типовых механизмов разработаны программы вычислений на ЭВМ.

Траектории отдельных точек механизма определяют обычно совместно с определением положений звеньев, причём выполняется графическое построение или аналитическое исследование только тех траекторий, от вида которых зависит движение рабочих органов механизма. Траектории, описываемые точками механизма, весьма разнообразны и в некоторых случаях представляют собой сложные плоские или пространственные кривые. Например, траектория, описываемая точкой М ( рис. 1 ), является алгебраической кривой 6-го порядка. Траектории точек, лежащих на звене ME, представляют уже кривые 14-го порядка.

Определение скоростей звеньев и отдельных точек механизмов — наиболее разработанный раздел К. м., располагающий графическими методами кинематических диаграмм и планов скоростей и аналитическим методом. Для определения скоростей какой-либо точки строят диаграмму изменения пути этой точки по времени, используя данные, полученные при определении положений звеньев, а затем, применяя графическое дифференцирование, строят диаграмму изменения скорости по времени (см. Графические вычисления ). Это метод наиболее простой, однако характеризуется небольшой точностью. Метод планов скоростей применим для плоских и пространственных механизмов. При построении планов скоростей используют соотношения между векторами скоростей различных точек механизма. Точность метода планов скоростей, как и всякого графического метода, ограничена, поэтому при исследовании механизмов, для которых требуется повышенная точность кинематического расчёта, предпочтительно применение аналитических методов, которые всегда можно свести к системе линейных уравнений.