БСЭ БСЭ - Большая Советская Энциклопедия (КИ)

Для получения телевизионных изображений на большом экране (площадью 3—4 м 2) выпускаются проекционные К. с диаметром экрана 6, 10, 13 см и высокой яркостью его свечения (25—30 тыс. нт ) при силе тока луча 100—150 мка (для 6 и 10 -см экранов) и 2000 мка (для 13- см экрана).

Лит.: Телевидение под ред. П. В. Шмакова. 3 изд., М.,1970; Жигарев А. А., Электронная оптика и электроннолучевые приборы, М., 1972.

В. И. Баранов.

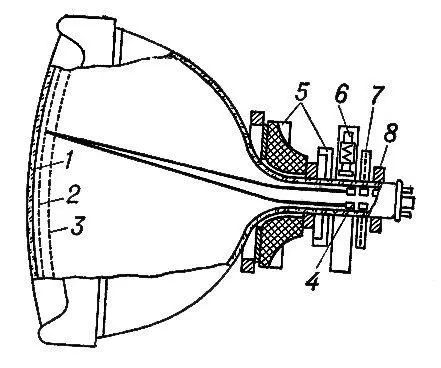
Рис. 2. Схематическое устройство цветного кинескопа с теневой маской типа 59ЛКЗЦ: 1 — экран; 2 — люминофорные точки (триады); 3 — мелкоструктурная цветоделительная маска; 4 — электронный прожектор; 5 — отклоняющая система; 6 — система радиального свечения; 7 — магнит чистоты цвета; 8 — магнит смещения луча.

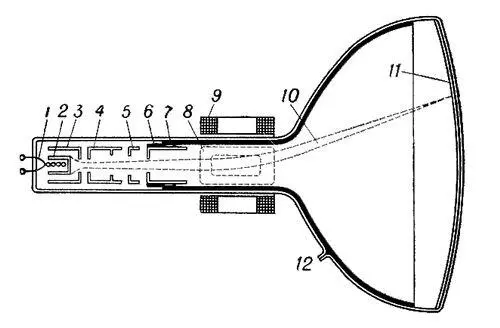
Рис. 1. Схематическое устройство кинескопа для черно-белого телевидения: 1 — нить подогревателя катода; 2 — катод; 3 — управляющий электрод; 4 — ускоряющий электрод; 5 — первый анод; 6 — второй анод; 7 — проводящее покрытие (акводаг); 8 — катушки вертикального отклонения луча; 9 — катушки горизонтального отклонения луча; 10 — электронный луч; 11 — экран; 12 — вывод второго анода.

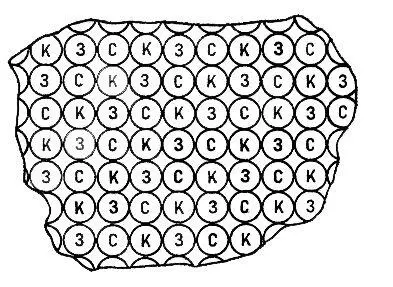
Рис. 3. Мозаика (триады) экрана цветного кинескопа с теневой маской: К — красные, З — зелёные, С — синие люминофорные «точки».

Кине'тика(от греч. kinetikós — приводящий в движение) основная часть механики , включающая динамику— учение о движении тел под действием сил и статики— учение о равновесии тел пол действием сил.

«Кине'тика и ката'лиз»,научный журнал, орган Сибирского отделения АН СССР. Издается в Москве с 1960. Выходит 6 номеров в год. В журнале публикуются оригинальные теоретические и экспериментальные работы по кинетике химических превращений в газах, растворах и твердых фазах, по исследованию промежуточных активных частиц (радикалов, ионов), горению, механизму гомогенного и гетерогенного катализа, по научным основам подбора катализаторов, практически важным каталитическим процессам, влиянию процессов переноса вещества и тепла на кинетику химических превращении, по методике расчета и моделирования контактных аппаратов. Печатаются также обзоры по важнейшим вопросам катализа и кинетики химических превращений. Тираж (1972) 1650 экз.

Кине'тика физи'ческая,теория неравновесных макроскопических процессов, то есть процессов, возникающих в системах, выведенных из состояния теплового (термодинамического) равновесия. К К. ф. можно отнести термодинамику неравновесных процессов, кинетическую теорию газов (в том числе плазмы), теорию процессов переноса в твёрдых телах, а также общую статистическую теорию неравновесных процессов, которая начала развиваться лишь в 50-е гг.

Все неравновесные процессы в адиабатически изолированных системах (системах, не обменивающихся теплом с окружающими телами) являются необратимыми процессами — происходят с увеличением энтропии ; в равновесном состоянии энтропия достигает максимума.

Как и в случае равновесных состояний, в К. ф. возможны два способа описания систем: феноменологический, или термодинамический (термодинамика неравновесных процессов), и статистический.

Термодинамический метод описания неравновесных процессов

При термодинамическом описании неравновесных процессов рассматривается изменение в пространстве и времени таких макроскопических параметров состояния системы, как плотность массы i -го компонента r i ( r, t ) , плотность импульса ru ( r, t ) , локальная температура T ( r , t ) , поток массы i-го компонента j i ( r, t ) , плотность потока внутренней энергии q ( r, t ) [здесь r — координата, t — время, u — средняя массовая скорость, r — плотность массы]. В равновесном состоянии системы r , r i, Т постоянны, а потоки равны нулю.

Термодинамическое описание неравновесных возможно лишь при достаточно медленном параметров состояния в пространстве и во времени для состояний, близких к равновесным. Для газов это означает, что все термодинамические параметры, характеризующие состояние системы, мало меняются на длине свободного пробега и за время, равное среднему времени свободного пробега молекул (среднему времени между двумя последовательными столкновениями молекул). Медленные процессы встречаются практически очень часто, так как установление равновесия происходит только после очень большого числа столкновений; к ним относятся: диффузия, теплопроводность, электропроводность и т.д. Отклонения от состояния термодинамического равновесия характеризуются градиентами температуры, концентрации ( r i/r ) и массовой скорости (так называемыми термодинамическими силами), а потоки энергии, массы i -го компонента и импульса связаны с термодинамическими силами линейными соотношениями. Коэффициенты в этих соотношениях называются кинетическими коэффициентами.

Рассмотрим в качестве примера диффузию в бинарной смеси, то есть процесс выравнивания концентрации компонентов в результате хаотического теплового движения молекул. Феноменологическое уравнение, описывающее процесс диффузии, получают с помощью закона сохранения вещества и того опытного факта, что поток вещества одного из компонентов вследствие диффузии прямо пропорционален градиенту его концентрации (с обратным знаком). Коэффициент пропорциональности называется коэффициентом диффузии. Согласно уравнению диффузии, скорость изменения концентрации вещества со временем прямо пропорциональна дивергенции градиента концентрации с коэффициентом пропорциональности, равным коэффициенту диффузии.

Решение уравнения диффузии позволяет определить время, в течение которого произойдёт выравнивание концентрации молекул в системе (например, в сосуде с газом) за счёт диффузии (время релаксации). Время релаксации t римеет порядок: t р~ L 2/D, где L — линейные размеры сосуда, a D — коэффициент диффузии. Это время тем больше, чем больше размеры сосуда и чем меньше коэффициент диффузии. Коэффициент диффузии пропорционален длине свободного пробега молекул l и их средней тепловой скорости n. Поэтому время релаксации оказывается пропорциональным: t р~ L 2/ ln = ( L/l ) 2l/n, где l/n = t — среднее время свободного пробега. Очевидно, что t р>> t при L >> l . Таким образом, условие L >> l (размеры системы велики по сравнению с длиной свободного пробега молекул) является необходимым для того, чтобы процесс установления равновесного состояния можно было считать медленным. Аналогичным образом устанавливаются уравнения, описывающие теплопроводность, внутреннее трение, электропроводность и т.д. Коэффициент диффузии, теплопроводности и вязкости, а также удельная электропроводность в феноменологической теории должны быть определены экспериментально.