БСЭ БСЭ - Большая Советская Энциклопедия (КИ)

Перечисленные процессы называются прямыми. Этим подчёркивается, что, например, при диффузии градиент концентрации данного вещества вызывает поток этого же вещества; градиент температуры вызывает поток внутренней энергии, которая при постоянной концентрации молекул меняется только с температурой; электрический ток вызывается градиентом потенциала и т.д. Кроме прямых процессов, существуют ещё так называемые перекрёстные процессы. Примером перекрёстного процесса может служить термодиффузия — перенос вещества не вследствие градиента концентрации (это была бы обычная диффузия), а вследствие градиента температуры. Термодиффузия создаёт градиент концентрации, что приводит к появлению обычной диффузии. Если разность температур в системе поддерживается постоянной, то устанавливается стационарное состояние, при котором потоки вещества, вызванные градиентами температуры и концентрации, взаимно уравновешиваются. В смеси газов при этом концентрация молекул в местах повышенной температуры оказывается большей для молекул меньшей массы (данное явление используется для разделения изотопов ) .

Градиент концентрации в свою очередь создаёт поток внутренней энергии. В этом состоит процесс диффузионной теплопроводности. При наличии в теле заряженных частиц градиент температуры создаёт упорядоченное перемещение этих частиц — электрический ток, называемый термоэлектрическим (см. Термоэлектрические явления ).

В К. ф. важное значение имеет принцип симметрии кинетических коэффициентов, установленный Л. Онсагером. В равновесном состоянии термодинамические параметры a i(давление, температура и т.д.), характеризующие состояние макроскопической системы, постоянны во времени: da i/dt = 0. Важнейшая функция состояния системы — энтропия S , зависящая от a i, в состоянии равновесия имеет максимум и, следовательно, её частные производные ¶S/¶ aj = 0. При малом отклонении системы от равновесия производные ¶S/¶ aj и ¶a/¶t малы, но отличны от нуля, и между ними существуют приближённые линейные соотношения. Коэффициенты пропорциональности в этих соотношениях и есть кинетические коэффициенты. Если через g ikобозначить коэффициент, определяющий скорость изменения параметра системы a i зависимости от 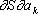, то, согласно принципу Онсагера (в отсутствие магнитного поля и вращения системы как целого), имеет место равенство g ik = g ki. Принцип Онсагера вытекает из свойства микроскопической обратимости, которая выражается в инвариантности уравнений движения частиц системы относительно замены знака времени: t ® — t (см. Онсагера теорема ) . Из этого принципа, в частности, следует существование связи между коэффициентами, определяющим выделение током тепла из-за неравномерного нагрева проводника (Томсона эффект), и коэффициентами, определяющим выделение током тепла в спаях разнородных проводников или полупроводников (Пельтье эффект).

Статистический метод описания неравновесных процессов.

Статистическая теория неравновесных процессов является более детальной и глубокой, чем термодинамическая. В отличие от термодинамического метода, статистическая теория на основе определенных представлений о строении вещества и действующих между молекулами силах позволяет вычислить кинетические коэффициенты, определяющие интенсивность процессов диффузии, внутреннего трения ( вязкости ) , электропроводности и т.д. Однако эта теория весьма сложна.

Статистический метод описания систем как в равновесном, так и неравновесном состоянии основан на вычислении функции распределения. Для равновесных состояний имеются универсальные функции распределения координат и импульсов (или скоростей) всех частиц, определяющие вероятность того, что эти величины принимают фиксированные значения. Для систем, находящихся в тепловом контакте с окружающей средой, температура которой постоянна, это — каноническое Гиббса распределение, а для изолированных систем — микроканоническое Гиббса распределение; оба распределения полностью определяются энергией системы.

Неравновесные состояния в гораздо большей степени (чем равновесные) зависят от микроскопических свойств систем: свойств атомов и молекул и сил взаимодействия между ними. Лишь в 50—60-е гг. были разработаны общие методы построения функций распределения (по координатам и импульсам всех частиц системы), аналогичных каноническому распределению Гиббса, но описывающих неравновесные процессы.

С помощью функций распределения можно определить любые макроскопические величины, характеризующие состояние системы, и проследить за их изменением в пространстве с течением времени. Это достигается вычислением статистических средних (см. Статистическая физика ) . Нахождение функции распределения, зависящей от координат и импульсов всех частиц, является в общем случае неразрешимой задачей, т.к. оно эквивалентно решению уравнений движения для всех частиц системы. Однако для практических целей нет необходимости в знании точного вида этой функции распределения: она содержит слишком подробную информацию о движении отдельных частиц, которая не существенна для определения поведения системы в целом. В связи с этим используется приближенное статистическое описание с помощью более простых функций распределения. Для описания состояния газов средней плотности достаточно знания так называемой одночастичной функции распределения f ( p, r, t ), дающей среднее число частиц с определёнными значениями импульсов р (или скоростей n ) и координат r. Для газов более высокой плотности необходимо знание двухчастичных (парных) функций распределения. Общий метод получения уравнений для одночастичных и более сложных функций (зависящих от координат и импульсов двух и более частиц) был разработан Н. Н. Боголюбовым, М. Борном, М. Грином и др. Эти уравнения называются кинетическими. К их числу относится кинетическое уравнение Больцмана для разреженных газов, полученное Л. Больцманом из соображений, основанных на балансе частиц со скоростями в интервалах D n x , D n y , D n z внутри объёма D х D y D z ( n x , n y , n z — проекции скорости n на координатные оси х, у, z ) . Разновидностями уравнения Больцмана для ионизированного газа (плазмы) являются кинетические уравнения Л. Д. Ландау и А. А. Власова (см. Плазма ) .

Кинетические уравнения могут быть построены не только для газов, но и для малых возбуждений в конденсированных системах. Тепловое движение системы характеризуется различного рода возбуждениями. В газе это — поступательное движение составляющих его частиц и внутренние возбуждения атомов и молекул. В общем случае тепловое движение характеризуется возбуждениями более сложной природы. Так, в кристаллических телах тепловое возбуждение можно представить в виде упругих волн, распространяющихся вдоль кристалла, точнее — волн, соответствующих нормальным колебаниям кристаллической решётки. В плазме коллективными возбуждениями являются колебания плотности электрического заряда, вызванные дальнодействующими кулоновскими силами. В металлах возможны электронные возбуждения (переходы электронов из состояний внутри Ферми поверхности в состояния вне её), а в полупроводниках — ещё и дырочные возбуждения (появление свободных от электронов состояний в валентной зоне при переходе электронов в зону проводимости; см. Полупроводники ) . При низких температурах, в слабовозбуждённом состоянии, энергию возбуждения всегда можно представить в виде суммы некоторых элементарных возбуждений, или, на квантовом языке, квазичастиц. Понятие о квазичастицах применимо не только для кристаллических тел, но и для жидких, газообразных и аморфных, если температура не слишком велика. Функции распределения для квазичастиц системы, находящейся в неравновесном состоянии, удовлетворяют кинетическому уравнению.