БСЭ БСЭ - Большая Советская Энциклопедия (КВ)

Т о., квантовомеханические представления впервые дали возможность теоретически оценить размеры атома (выразив его радиус через мировые постоянные 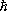, m, е ). «Малость» атомных размеров оказалась связанной с тем, что «мала» постоянная .

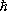Примечательно, что современные представления об атомах, обладающих вполне определёнными устойчивыми состояниями, оказываются ближе к представлениям древних атомистов, чем основанная на законах классической механики планетарная модель атома, позволяющая электрону находиться на любых расстояниях от ядра.

Строгое решение задачи о движении электрона в атоме водорода получается из квантовомеханического уравнения движения — уравнения Шрёдингера (см. ниже); решение уравнения Шрёдингера даёт волновую функцию y, которая описывает состояние электрона, находящегося в области притяжения ядра. Но и не зная явного вида y, можно утверждать, что эта волновая функция представляет собой такую суперпозицию волн де Бройля, которая соответствует локализации электрона в области с размером ³ r 0и разбросу по импульсам .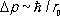

Соотношение неопределённостей позволяет также понять устойчивость молекул и оценить их размеры и минимальную энергию, объясняет существование вещества, которое ни при каких температурах не превращается при нормальном давлении в твёрдое состояние (гелий), даёт качественное представления о структуре и размерах ядра и т.д.

Существование уровней энергии — характерное квантовое явление, присущее всем физическим системам, не вытекает непосредственно из соотношения неопределённостей. Ниже будет показано, что дискретность уровней энергии связанной системы можно объяснить на основе уравнения Шрёдингера; отметим лишь, что возможные дискретные значения энергии (энергетические уровни) E n> E 0соответствуют возбуждённым состояниям квантовомеханической системы (см., например, Атом ).

Стационарное уравнение Шрёдингера.Волны де Бройля описывают состояние частицы только в случае свободного движения. Если на частицу действует поле сил с потенциальной энергией V (называемой также потенциалом), зависящей от координат частицы, то волновая функция частицы y определяется дифференциальным уравнением, которое получается путём следующего обобщения гипотезы де Бройля. Для случая, когда движение частицы с заданной энергией E происходит в одном измерении (вдоль оси х ), уравнение,. которому удовлетворяет волна де Бройля (5), может быть записано в виде:

, (*)

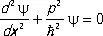где 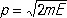— импульс свободно движущейся частицы (массы m ). Если частица с энергией E движется в потенциальном поле V ( x ), не зависящем от времени, то квадрат её импульса (определяемый законом сохранения энергии) равен 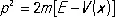. Простейшим обобщением уравнения (*) является поэтому уравнение

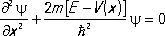. (7)

Оно называется стационарным (не зависящим от времени) уравнением Шрёдингера и относится к основным уравнениям К. м. Решение этого уравнения зависит от вида сил, т. е. от вида потенциала V ( x ). Рассмотрим несколько типичных случаев.

1) V = const, E > V . Решением является волна де Бройля y = Ce ikx, где 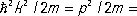E - V — кинетическая энергия частицы.

2) Потенциальная стенка:

V = 0 при х < 0,

V = V 1 > 0 при х > 0.

Если полная энергия частицы больше высоты стенки, т. е. E > V 1, и частица движется слева направо ( рис. 3 ), то решение уравнения (7) в области x < 0 имеет вид двух волн де Бройля — падающей и отражённой:

,

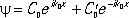где

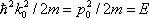
(волна с волновым числом k = – k 0соответствует движению справа налево с тем же импульсом p 0), а при х > 0 — проходящей волны де Бройля:

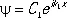, где .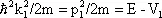

Отношения | C 1/ C 2| 2и | C' 0/ C 0| 2определяют вероятности прохождения частицы над стенкой и отражения от неё. Наличие отражения — специфически квантовомеханическое (волновое) явление (аналогичное частичному отражению световой волны от границы раздела двух прозрачных сред): «классическая» частица проходит над барьером, и лишь импульс её уменьшается до значения .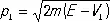

Если энергия частицы меньше высоты стенки, E < V ( рис. 4, а ), то кинетическая энергия частицы E — V в области х > 0 отрицательна. В классической механике это невозможно, и частица не заходит в такую область пространства — она отражается от потенциальной стенки. Волновое движение имеет др. характер. Отрицательное значение 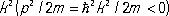означает, что k — чисто мнимая величина, k = i c , где c вещественно. Поэтому волна e ikxпревращается в e — c x, т. е. колебательный режим сменяется затухающим (c > 0, иначе получился бы лишённый физического смысла неограниченный рост волны с увеличением х ). Это явление хорошо известно в теории колебаний. Под энергетической схемой на рис. 4, а (и рис. 4, б ) изображено качественное поведение волновой функции y( х ), точнее её действительной части.

3) Две области, свободные от сил, разделены прямоугольным потенциальным барьеромV , и частица движется к барьеру слева с энергией E < V ( рис. 4, б ). Согласно классической механике, частица отразится от барьера; согласно К. м., волновая функция не равна нулю и внутри барьера, а справа будет опять иметь вид волны де Бройля с тем же импульсом (т. е. с той же частотой, но, конечно, с меньшей амплитудой). Следовательно, частица может пройти сквозь барьер. Коэффициент (или вероятность) проникновения будет тем больше, чем меньше ширина и высота (чем меньше разность V — E ) барьера. Этот типично квантовомеханический эффект, называемый туннельным эффектом , имеет большое значение в практических приложениях К. м. Он объясняет, например, явление альфа-распада— вылета из радиоактивных ядер a-частиц (ядер гелия). В термоядерных реакциях, протекающих при температурах в десятки и сотни млн. градусов, основная масса реагирующих ядер преодолевает электростатическое (кулоновское) отталкивание и сближается на расстояния порядка действия ядерных сил в результате туннельных (подбарьерных) переходов. Возможность туннельных переходов объясняет также автоэлектронную эмиссию — явление вырывания электронов из металла электрическим полем, контактные явления в металлах и полупроводниках и многие др. явления.