БСЭ БСЭ - Большая Советская Энциклопедия (КВ)

Следует подчеркнуть различие в смысле, вкладываемом в принцип суперпозиции в оптике (и др. волновых процессах) и К. м. Сложение (суперпозиция) обычных волн не противоречит наглядным представлениям, т.к. каждая из волн представляет возможный тип колебаний и суперпозиция соответствует сложению этих колебаний в каждой точке. В то же время квантовомеханические амплитуды вероятности описывают альтернативные (с классической точки зрения, исключающие друг друга) движения (например, волны y 1и y 2соответствуют частицам, приходящим в детектор двумя различными путями). С классической точки зрения, сложение таких движений представляется совершенно непонятным. В этом проявляется отсутствие наглядности квантовомеханического принципа суперпозиции. Избежать формального логического противоречия квантовомеханического принципа суперпозиции (возможность для частицы пройти одновременно двумя путями) позволяет вероятностная интерпретация. Постановка опыта по определению пути частицы (см. выше) приведёт к тому, что с вероятностью |y 1| 2частица пройдёт первым и с вероятностью |y 2| 2— вторым путём. Суммарное распределение частиц на экране будет определяться вероятностью |y 1| 2+ |y 2| 2, т. е. интерференция исчезнет.

Т. о., рассмотрение интерференционного опыта приводит к следующему выводу. Величиной, описывающей состояние физической системы в К. м., является амплитуда вероятности, или волновая функция, системы. Основная черта такого квантовомеханического описания — предположение о справедливости принципа суперпозиции состояний.

Принцип суперпозиции — основной принцип К. м. В общем виде он утверждает, что если в данных условиях возможны различные квантовые состояния частицы (или системы частиц), которым соответствуют волновые функции y 1, y 2,..., y i,..., то существует и состояние, описываемое волновой функцией

,

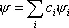где c i — произвольные комплексные числа. Если y iописывают альтернативные состояния, то | c i | 2определяет вероятность того, что система находится в состоянии с волновой функцией y i, и

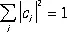
Волны де Бройля и соотношение неопределённостей.Одна из основных задач К. м. — нахождение волновой функции, отвечающей данному состоянию изучаемой системы. Рассмотрим решение этой задачи на простейшем (но важном) случае свободно движущейся частицы. Согласно де Бройлю, со свободной частицей, имеющей импульс р связана волна с длиной l = h / p . Это означает, что волновая функция свободной частицы y( х ) — волна де Бройля — должна быть такой функцией координаты х , чтобы при изменении х на l волновая функция y возвращалась к прежнему значению. Этим свойством обладает функция e i2 p x/l. Если ввести величину k = 2p/l, называемую волновым числом, то соотношение де Бройля примет вид: 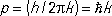. Т. о., если частица имеет определённый импульс р , то её состояние описывается волновой функцией

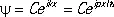, (5)

где С — постоянное комплексное число. Эта волновая функция обладает замечательным свойством: квадрат её модуля |y 1| 2не зависит от х , т. е. вероятность нахождения частицы, описываемой такой волновой функцией, в любой точке пространства одинакова. Другими словами, частица со строго определённым импульсом совершенно нелокализована. Конечно, это идеализация — полностью нелокализованных частиц не существует. Но в той же мере идеализацией является и волна со строго определённой длиной волны, а следовательно, и строгая определённость импульса частицы. Поэтому точнее сказать иначе: чем более определённым является импульс частицы, тем менее определенно её положение (координата). В этом заключается специфический для К. м. принцип неопределённости. Чтобы получить количественное выражение этого принципа — соотношение неопределённостей, рассмотрим состояние, представляющее собой суперпозицию некоторого (точнее, бесконечно большого) числа де-бройлевских волн с близкими волновыми числами, заключёнными в малом интервале D k . Получающаяся в результате суперпозиции волновая функция y( х ) (она называется волновым пакетом ) имеет такой характер: вблизи некоторого фиксированного значения x 0 все амплитуды сложатся, а вдали от x 0 (| х — x 0| >> l) будут гасить друг друга из-за большого разнобоя в фазах. Оказывается, что практически такая волновая функция сосредоточена в области шириной D х , обратно пропорциональной интервалу D k , т. е. D х » 1/D k , или 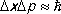(где 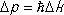— неопределённость импульса частицы). Это соотношение и представляет собой соотношение неопределённостей Гейзенберга.

Математически любую функцию y( х ) можно представить как наложение простых периодических волн — это известное Фурье преобразование , на основании свойств которого соотношение неопределённостей между D х и D k получается математически строго. Точное соотношение имеет вид неравенства D х D k ³ 1/ 2, или

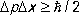, (6)

причём под неопределённостями D р и D х понимаются дисперсии, т. е. среднеквадратичные отклонения импульса и координаты от их средних значений. Физическая интерпретация соотношения (6) заключается в том, что (в противоположность классической механике) не существует такого состояния, в котором координата и импульс частицы имеют одновременно точные значения. Масштаб неопределённостей этих величин задаётся постоянной Планка 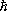, в этом заключён важный смысл этой мировой постоянной. Если неопределённости, связанные соотношением Гейзенберга, можно считать в данной задаче малыми и пренебречь ими, то движение частицы будет описываться законами классической механики (как движение по определённой траектории).

Принцип неопределённости является фундаментальным принципом К. м., устанавливающим физическое содержание и структуру её математического аппарата. Кроме этого, он играет большую эвристическую роль, т.к. многие результаты К. м. могут быть получены и поняты на основе комбинации законов классической механики с соотношением неопределённостей. Важным примером является проблема устойчивости атома, о которой говорилось выше. Рассмотрим эту задачу для атома водорода. Пусть электрон движется вокруг ядра (протона) по круговой орбите радиуса r со скоростью u. По закону Кулона сила притяжения электрона к ядру равна e 2/ r 2, где е — абсолютная величина заряда электрона, а центростремительное ускорение равно u 2/ r . По второму закону Ньютона m u 2 r = e 2/ r 2, где m — масса электрона. Отсюда следует, что радиус орбиты r = е 2 /m u 2может быть сколь угодно малым, если скорость u достаточно велика. Но в К. м. должно выполняться соотношение неопределённостей. Если допустить неопределённость положения электрона в пределах радиуса его орбиты r , а неопределённость скорости — в пределах u, т. е. импульса в пределах D р = m u, то соотношение неопределённостей примет вид: 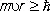. Воспользовавшись связью между u и r , определяемой законом Ньютона, получим 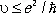и 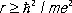. Следовательно, движение электрона по орбите с радиусом, меньшим 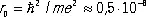см, невозможно, электрон не может упасть на ядро — атом устойчив. Величина r 0и является радиусом атома водорода («боровским радиусом»). Ему соответствует максимально возможная энергия связи атома E 0(равная полной энергии электрона в атоме, т. е. сумме кинетической энергии m u 2/2 и потенциальной энергии — e 2/ r 0, что составляет E 0» -13,6 эв ), определяющая его минимальную энергию — энергию основного состояния.