БСЭ БСЭ - Большая Советская Энциклопедия (КВ)

то E = 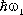с вероятностью ½ C 1½ 2и E = 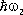с вероятностью ½ C 2½ 2. Для энергии и времени существует соотношение неопределенностей:

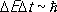, (11)

где D E — дисперсия энергии, а D t — промежуток времени, в течение которого энергия может быть измерена.

Трехмерное движение. Момент количества движения.До сих пор рассматривалось (ради простоты) одномерное движение. Обобщение на движение частицы в трех измерениях не содержит принципиально новых элементов. В этом случае волновая функция зависит от трех координат х , у, z (и времени): y = y ( х, у, z, t ), а волна де Бройля имеет вид

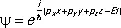, (12)

где p x, p y, p z,— три проекции импульса на оси координат, а 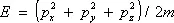. Соответственно имеются при соотношения неопределенностей:

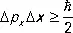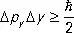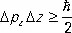, , , (13)

Временное уравнение Шредингера имеет вид:

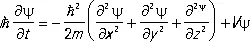. (14)

Это уравнение принято записывать в символической форме

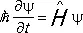, (14, a)

где

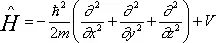
— дифференциальный оператор, называемый оператором Гамильтона, или гамильтонианом.

Стационарным решением уравнения (14) является:

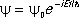, (15)

где y 0— решение уравнения Шредингера для стационарных состояний:

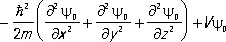= E y 0 (16)

или

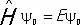. (16,а)

При трёхмерном движении спектр энергии также может быть непрерывным и дискретным. Возможен и случай, когда несколько разных состояний имеют одинаковую энергию; такие состояния называются вырожденными. В случае непрерывного спектра частица уходит на бесконечно большое расстояние от центра сил. Но, в отличие от одномерного движения (когда были только две возможности — прохождение или отражение), при трёхмерном движении частица может удалиться от центра под произвольным углом к направлению первоначального движения, т. е. рассеяться. Волновая функция частицы теперь является суперпозицией не двух, а бесконечного числа волн де Бройля, распространяющихся по всевозможным направлениям. Рассеянные частицы удобно описывать в сферических координатах, т. е. определять их положение расстоянием от центра (радиусом) r и двумя углами — широтой q и азимутом j. Соответствующая волновая функция на больших расстояниях r от центра сил имеет вид:

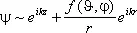. (17)

Первый член (пропорциональный волне де Бройля, распространяющейся вдоль оси z ) описывает падающие частицы, а второй (пропорциональный «радиальной волне де Бройля») — рассеянные. Функция f (J, j) называется амплитудой рассеяния; она определяет так называемое дифференциальное сечение рассеяния d s, характеризующее вероятность рассеяния под данными углами:

d s = | f (J, j)| 2 d W, (18)

где d W — элемент телесного угла, в который происходит рассеяние.

Дискретный спектр энергии возникает, как и при одномерном движении, когда частица оказывается внутри потенциальной ямы. Энергетические уровни нумеруют квантовыми числами, причём, в отличие от одномерного движения, не одним, а тремя. Наибольшее значение имеет задача о движении в поле центральных сил притяжения. В этом случае также удобно пользоваться сферическими координатами.

Момент количества движения.Угловая часть движения (вращение) определяется в К. м., как и в классической механике, заданием момента количества движения, который при движении в поле центральных сил сохраняется. Но, в отличие от классической механики, в К. м. момент имеет дискретный спектр, т. е. может принимать только вполне определённые значения. Это можно показать на примере азимутального движения — вращения вокруг заданной оси (примем её за ось z ). Волновая функция в этом случае имеет вид «угловой волны де Бройля» e im j, где j — азимут, а число m также связано с моментом M z, как в плоской волне де Бройля волновое число k с импульсом р , т. е. m = M z/ h . Т. к. углы j и j + 2p описывают одно и то же положение, то и волновая функция при изменении j на 2p должна возвращаться к прежнему значению. Отсюда вытекает, что m может принимать только целочисленные значения: m = 0, ± 1, ± 2,..., т. е. момент может быть равен

M z = mh = 0, ± h , ± 2 h ,... (19)

Вращение вокруг оси z есть только часть углового движения (это проекция движения на плоскость ху ), а M z — не полный момент, а только его проекция на ось z . Чтобы узнать полный момент, надо определить две остальные его проекции. Но в К. м. нельзя одновременно точно задать все три составляющие момента. Действительно, проекция момента содержит произведение проекции импульса на соответствующее плечо (координату, перпендикулярную импульсу), а все проекции импульса и все плечи, согласно соотношениям неопределённостей (13), одновременно не могут иметь точные значения. Оказывается, что, кроме проекции M zмомента количества движения на ось z (задаваемой числом m ), можно одновременно точно задать величину момента М , определяемую целым числом l :

M 2= h 2 l ( l + 1), l = 0, 1, 2,... (20)

Т. о., угловое движение даёт два квантовых числа — l и m . Число l называют орбитальным квантовым числом, от него может зависеть значение энергии частицы (как в классической механике от вытянутости орбиты). Число m называют магнитным квантовым числом и при данном l может принимать значения m = 0, ± 1, ± 2,..., ± l — всего 2 l + 1 значений; от m энергия не зависит, т.к. само значение m зависит от выбора оси z , а поле имеет сферическую симметрию. Поэтому уровень с квантовым числом l имеет (2 l + 1)-кратное вырождение. Энергия уровня начинает зависеть от m лишь тогда, когда сферическая симметрия нарушается, например при помещении системы в магнитное поле ( Зеемана эффект ).