БСЭ БСЭ - Большая Советская Энциклопедия (КВ)

,

.

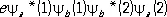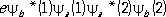Она называется обменной плотностью, потому что возникает как бы за счёт обмена электронами между двумя атомами. Именно эта обменная плотность, приводящая к увеличению плотности отрицательного заряда между двумя положительно заряженными ядрами, и обеспечивает устойчивость молекулы в случае ковалентной химической связи.

Очевидно, что при суммарном спине двух электронов, равном 1, координатная часть волновой функции антисимметрична, т. е. в (25) перед вторым слагаемым стоит знак минус, и обменная плотность имеет отрицательный знак; это означает, что обменная плотность будет уменьшать плотность отрицательного электрического заряда между ядрами, т. е. приводить как бы к дополнительному отталкиванию ядер.

Т. о., симметрия волновой функции приводит к «дополнительному» обменному взаимодействию . Характерна зависимость обменного взаимодействия от спинов электронов. Непосредственно спины не участвуют во взаимодействии — источником взаимодействия являются электрические силы, зависящие только от расстояния между зарядами. Но в зависимости от ориентации спинов волновая функция, антисимметричная относительно полной перестановки двух электронов (вместе с их спинами), может быть симметричной или антисимметричной относительно перестановки только положения электронов (их координат). А от типа симметрии координатной части волновой функции зависит знак обменной плотности и, соответственно, эффективное притяжение или отталкивание частиц в результате обменного взаимодействия. Так, не участвуя непосредственно динамически во взаимодействии, спины электронов благодаря квантовомеханической специфике свойств тождественных частиц фактически определяют химическую связь.

Обменное взаимодействие играет существенную роль во многих явлениях. Оно объясняет, например, ферромагнетизм: благодаря обменному взаимодействию спиновые, а следовательно, и магнитные моменты атомов ферромагнетика выстраиваются параллельно друг другу. Огромное число явлений в конденсированных телах (жидкости, твёрдом теле) тесно связано со статистикой образующих их частиц и с обменным взаимодействием. Условие антисимметрии волновой функции для фермионов приводит к тому, что фермионы при большой плотности как бы эффективно отталкиваются друг от друга (даже если между ними не действуют никакие силы). В то же время между бозонами, которые описываются симметричными волновыми функциями, возникают как бы силы притяжения: чем больше бозонов находится в каком-либо состоянии, тем больше вероятность перехода др. бозонов системы в это состояние (подобного рода эффекты лежат, например, в основе явлений сверхтекучести и сверхпроводимости, принципа работы квантовых генераторов и квантовых усилителей ).

Математическая схема квантовой механики.Нерелятивистская К. м. может быть построена на основе немногих формальных принципов. Математический аппарат К. м. обладает логической безупречностью и изяществом. Чёткие правила устанавливают соотношение между элементами математической схемы и физическими величинами.

Первым основным понятием К. м. является квантовое состояние. Выбор математического аппарата К. м. диктуется физическим принципом суперпозиции квантовых состояний, вытекающим из волновых свойств частиц. Согласно этому принципу, суперпозиция любых возможных состояний системы, взятых с произвольными (комплексными) коэффициентами, является также возможным состоянием системы. Объекты, для которых определены понятия сложения и умножения на комплексное число, называется векторами. Т. о., принцип суперпозиции требует, чтобы состояние системы описывалось некоторым вектором — вектором состояния (с которым тесно связано понятие амплитуды вероятности, или волновой функции), являющимся элементом линейного «пространства состояний». Это позволяет использовать математический аппарат, развитый для линейных (векторных) пространств. Вектор состояния обозначается по П. Дираку .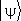

Кроме сложения и умножения на комплексное число, вектор 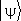может подвергаться ещё двум операциям. Во-первых, его можно проектировать на др. вектор, т. е. составить скалярное произведение 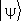с любым др. вектором состояния 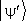; оно обозначается как 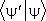и является комплексным числом, причём

= * . (26)

Скалярное произведение вектора 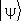с самим собой, 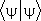, — положительное число; оно определяет длину (норму) вектора. Длину вектора состояния удобно выбрать равной единице; его общий фазовый множитель произволен. Различные состояния отличаются друг от друга направлением вектора состояния в пространстве состояний.

Во-вторых, можно рассмотреть операцию перехода от вектора 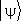к др. вектору 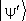(или произвести преобразование 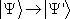). Символически эту операцию можно записать как результат действия на вектор 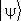некоторого линейного оператора :

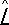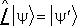(27)

При этом вектор 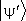может отличаться от 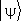«длиной» и «направлением». Линейные операторы, в силу принципа суперпозиции состояний, имеют в К. м. особое значение; в результате воздействия линейного оператора на суперпозицию произвольных векторов 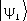и 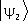получается суперпозиция преобразованных векторов:

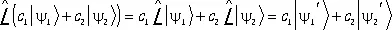. (28)

Важную роль для оператора 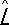играют такие векторы 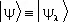, для которых 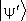совпадает по направлению с 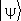, т. е.