БСЭ БСЭ - Большая Советская Энциклопедия (КВ)

Возможна такая математическая формулировка, в которой формальный переход от классической механики к К. м. осуществляется заменой с -чисел соответствующими q -числами. Сохраняются и уравнения движения, но теперь это уравнения для операторов. Из этой формальной аналогии между К. м. и классической механикой можно найти основные коммутационные (перестановочные) соотношения. Так, для координаты и импульса 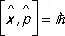. Отсюда следует соотношение неопределённостей Гейзенберга 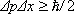. Из перестановочных соотношений можно получить, в частности, явный вид оператора импульса, в координатном ( х– ) представлении. Тогда волновая функция есть y( х ), а оператор импульса — дифференциальный оператор

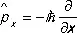, т. е. .

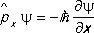Можно показать, что спектр его собственных значений непрерывен, а амплитуда вероятности 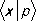есть де-бройлевская волна ( 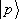— собственный вектор оператора импульса 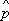). Если задана энергия системы как функция координат и импульсов частиц, Н ( р , х ), то знание коммутатора 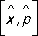достаточно для нахождения 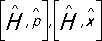, а также уровней энергии как собственных значений оператора полной энергии .

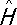На основании определения момента количества движения M z = хр у — ур х,... можно получить, что 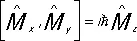. Эти коммутационные соотношения справедливы и при учёте спинов частиц; их оказывается достаточно для определения собственного значения квадрата полного момента: 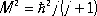, где квантовое число j — целое или полуцелое число, и его проекции 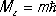, m = - j , - j + 1, …, + j .

Уравнения движения квантовомеханической системы могут быть записаны в двух формах: в виде уравнения для вектора состояния

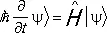(36)

— шрёдингеровская форма уравнения движения, и в виде уравнения для операторов ( q -чисел)

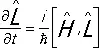(37)

— гейзенберговская форма уравнений движения, наиболее близкая классической механике. Из гейзенберговской формы уравнений движения, в частности, следует, что средние значения физических величин изменяются по законам классической механики; это положение называется теоремой Эренфеста.

Для логической структуры К. м. характерно присутствие двух совершенно разнородных по своей природе составляющих. Вектор состояния (волновая функция) однозначно определён в любой момент времени, если задан в начальный момент. В этой части теория вполне детерминистична. Но вектор состояния не есть наблюдаемая величина. О наблюдаемых на основе знания 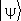можно сделать лишь статистические (вероятностные) предсказания. Результаты индивидуального измерения над квантовым объектом в общем случае, строго говоря, непредсказуемы. Предпринимались попытки восстановить идею полного детерминизма в классическом смысле введением предположения о неполноте квантовомеханического описания. Например, высказывалась гипотеза о наличии у квантовых объектов дополнительных степеней свободы — «скрытых параметров», учёт которых сделал бы поведение системы полностью детерминированным в смысле классической механики; неопределённость возникает только вследствие того, что эти «скрытые параметры» неизвестны и не учитываются. Однако Дж. Нейман доказал теорему о невозможности нестатистической интерпретации К. м. при сохранении её основного положения о соответствии между наблюдаемыми (физическими величинами) и операторами.

Лит.: Классич. труды — Гейзенберг В., Физические принципы квантовой теории, Л. — М., 1932; Дирак П., Принципы квантовой механики, пер. с англ., М., 1960; Паули В., Общие принципы волновой механики, пер. с нем., М. — Л., 1947; Нейман И., Математические основы квантовой механики, пер. с нем., М., 1964. Учебники — Ландау Л. Д., Лифшиц Е. М., Квантовая механика, 2 изд., М., 1963 (Теоретическая физика, т. 3); Блохинцев Д. И., Основы квантовой механики, 4 изд., М., 1963; Давыдов А. С., Квантовая механика, М., 1963; Соколов А. А., Лоскутов Ю. М., Тернов И. М., Квантовая механика, М., 1962; Бом Д., Квантовая теория, пер. с англ., М., 1961; Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике, пер. с англ., в. 8 и 9, М.,1966—67; Шифф Л., Квантовая механика, пер. с англ., 2 изд., М., 1959; Ферми Э., Квантовая механика, пер. с англ., М., 1965. Популярные книги — Борн М., Атомная физика, пер. с англ., 3 изд., М., 1970; Пайерлс Р. Е., Законы природы, пер. с англ., 2 изд., М., 1962.

В. Б. Берестецкий.

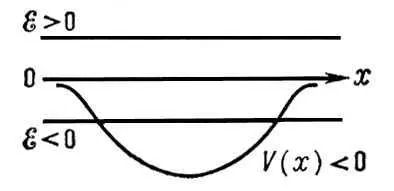
Рис. 5 к ст. Квантовая механика.

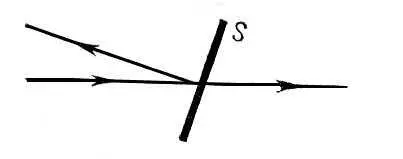
Рис. 1 к ст. Квантовая механика.

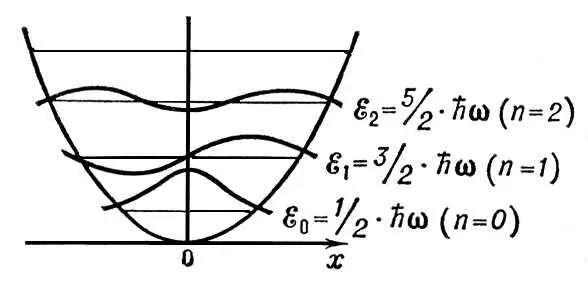
Рис. 6 к ст. Квантовая механика.

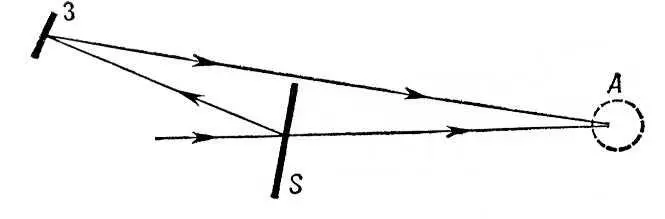
Рис. 2 к ст. Квантовая механика.

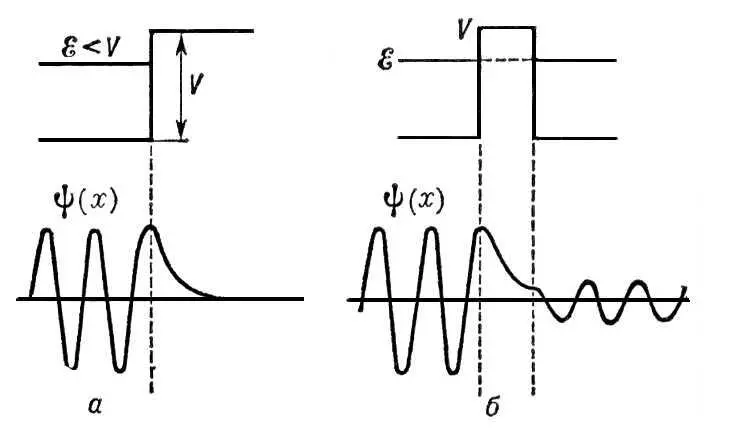
Рис. 4 к ст. Квантовая механика.

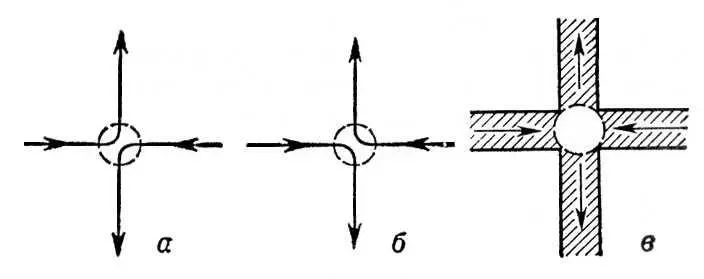
Рис. 7 к ст. Квантовая механика.

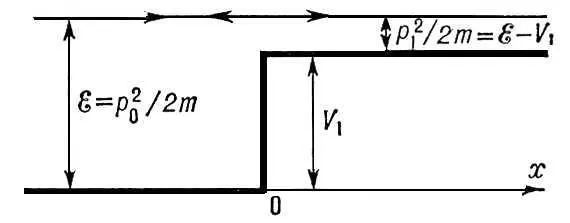
Рис. 3 к ст. Квантовая механика.

Ква'нтовая радиофи'зика,то же, что и квантовая электроника .