БСЭ БСЭ - Большая Советская Энциклопедия (КВ)

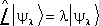(29)

Векторы 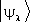называют собственными векторами оператора 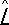, а числа l — его собственными значениями. Собственные векторы 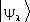принято обозначать просто 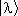, т. е. 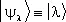. Собственные значения l образуют либо дискретный ряд чисел (тогда говорят, что оператор 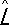имеет дискретный спектр), либо непрерывный набор (непрерывный спектр), либо частично дискретный, частично непрерывный.

Очень важный для К. м. класс операторов составляют линейные эрмитовы операторы . Собственные значения l эрмитового оператора 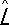вещественны. Собственные векторы эрмитового оператора, принадлежащие различным собственным значениям, ортогональны друг к другу, т. е.

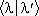= 0. (30)

Из них можно построить ортогональный базис («декартовы оси координат») в пространстве состояний. Удобно нормировать эти базисные векторы на 1, 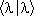=1. Произвольный вектор 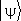можно разложить по этому базису:

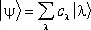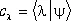; . (31)

При этом:

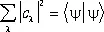, (32)

что эквивалентно теореме Пифагора; если 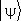нормирован на 1, то

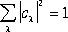. (33)

Принципиальное значение для построения математического аппарата К. м. имеет тот факт, что для каждой физической величины существуют некоторые выделенные состояния системы, в которых эта величина принимает вполне определённое (единственное) значение. По существу это свойство является определением измеримой (физической) величины, а состояния, в которых физическая величина имеет определённое значение, называются собственными состояниями этой величины.

Согласно принципу суперпозиции, любое состояние системы может быть представлено в виде суперпозиции собственных состояний какой-либо физической величины. Возможность такого представления математически аналогична возможности разложения произвольного вектора по собственным векторам линейного эрмитового оператора. В соответствии с этим в К. м. каждой физической величине, или наблюдаемой, L (координате, импульсу, моменту количества движения, энергии и т.д.) ставится в соответствие линейный эрмитов оператор 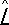. Собственное значение l оператора 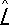интерпретируются как возможные значения физической величины L , проявляющиеся при измерениях. Если вектор состояния 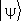— собственный вектор оператора 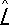, то физическая величина L имеет определённое значение. В противном случае L принимает различные значения l с вероятностью | c l| 2, где c l— коэффициент разложения 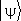по :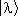

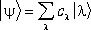. (34)

Коэффициент c l = 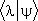разложения 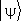в базисе 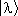называется также волновой функцией в l-представлении. В частности, волновая функция y( х ) представляет собой коэффициент разложения 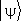по собственным векторам оператора координаты .

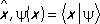Среднее значение 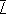наблюдаемой L в данном состоянии определяется коэффициентами с l, согласно общему соотношению между вероятностью и средним значением

.

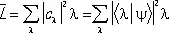Значение 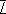можно найти непосредственно через оператор 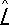и вектор состояния 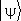(без определения коэффициентов с l) по формуле:

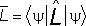. (35)

Вид линейных эрмитовых операторов, соответствующих таким физическим величинам, как импульс, момент количества движения, энергия, постулируется на основе общих принципов определения этих величин и соответствия принципа , требующего, чтобы в пределе 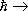0 рассматриваемые физические величины принимали «классические» значения. Вместе с тем в К. м. вводятся некоторые линейные эрмитовы операторы (например, отвечающие преобразованию векторов состояния при отражении осей координат, перестановке одинаковых частиц и т.д.), которым соответствуют измеримые физические величины, не имеющие классических аналогов (например, чётность ).

С операторами можно производить алгебраические действия сложения и умножения. Но, в отличие от обыкновенных чисел (которые в К. м. называют с -числами), операторы являются такими «числами» ( q -числами), для которых операция умножения некоммутативна. Есл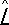и и — два оператора, то в общем случае их действие на произвольный вектор 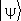в различном порядке даёт разные векторы: 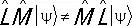, т. е. 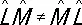. Величина 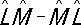обозначается как 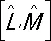и называется коммутатором. Только если два оператора переставимы (коммутируют), т. е. 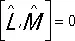, у них могут быть общие собственные векторы и, следовательно, наблюдаемые L и М могут одновременно иметь определённые (точные) значения l и m. В остальных случаях эти величины не имеют одновременно определённых значений, и тогда они связаны соотношением неопределённостей. Можно показать, что, если 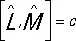, то D L D M ³ | c |/2, где D L и D М — среднеквадратичные отклонения от средних для соответствующих величин.