БСЭ БСЭ - Большая Советская Энциклопедия (КВ)

Взаимные превращения частиц, порождение одних и уничтожение других, можно количественно описывать при помощи так называемого метода вторичного квантования [предложенного в 1927 П. Дираком и получившего дальнейшее развитие в работах В. А. Фока (1932)].

2. Вторичное квантование.Переход от классической механики к квантовой называют просто квантованием, или реже — «первичным квантованием». Как уже говорилось, такое квантование не даёт возможности описывать изменение числа частиц в системе. Основной чертой метода вторичного квантования является введение операторов, описывающих порождение и уничтожение частиц. Поясним действие этих операторов на простом примере (или модели) теории, в которой рассматриваются одинаковые частицы, находящиеся в одном и том же состоянии (например, все фотоны считаются имеющими одинаковую частоту, направление распространения и поляризацию). Т. к. число частиц в данном состоянии может быть произвольным, то этот случай соответствует бозе-частицам, или бозонам ,

подчиняющимся Бозе — Эйнштейна статистике .

В квантовой теории состояние системы частиц описывается волновой функцией или вектором состояния. Введём для описания состояния с N частицами вектор состояния Y N; квадрат модуля Y N, |Y N| 2, определяющий вероятность обнаружения N частиц, обращается, очевидно, в 1, если N достоверно известно. Это означает, что вектор состояния с любым фиксированным N нормирован на 1. Введём теперь оператор уничтожения частицы а –и оператор рождения частицы а +. По определению, а –переводит состояние с N частицами в состояние с N —1 частицей, т. е.

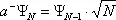(3)

Аналогично, оператор порождения частицы а +переводит состояние Y Nв состояние с N + 1 частицей:

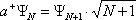, (4)

[множители 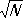в (3) и 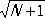в (4) вводятся именно для выполнения условия нормировки: |Y N| 2= 1]. В частности, при N = 0 а +Y 0= Y 1 , где Y 0— вектор состояния, характеризующий вакуум; т. е. одночастичное состояние получается в результате порождения из «вакуума» одной частицы. Однако а –Y 0= 0 , поскольку невозможно уничтожить частицу в состоянии, в котором частиц нет; это равенство можно считать определением вакуума. Вакуумное состояние Y 0имеет в К. т. п. особое значение, т.к. из него при помощи операторов а +можно получить любое состояние. Действительно, в рассматриваемом случае (когда состояние всей системы определяется только числом частиц)

,

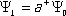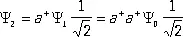, (5)

……………………………………

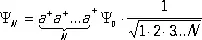
Легко показать, что порядок действия операторов а – и а + не безразличен. Действительно, а –(а +Y 0) = а –Y 1= Y 0 , в то время как а +(а –Y 0) = 0 . Т. о., (a –a +— a +a –)Y 0= Y 0 , или

a –a +—a +a –= 1 , (6)

т. е. операторы а + и а – являются непереставимыми (некоммутирующими). Соотношения типа (6), устанавливающие связь между действием двух операторов, взятых в различном порядке называется перестановочными соотношениями , или коммутационными соотношениями для этих операторов, а выражения вида 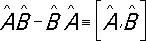— коммутаторами операторов и .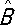

Если учесть, что частицы могут находиться в различных состояниях, то, записывая операторы порождения и уничтожения, надо дополнительно указывать, к какому состоянию частицы эти операторы относятся. В квантовой теории состояния задаются набором квантовых чисел , определяющих энергию, спин и др. физические величины; для простоты обозначим всю совокупность квантовых чисел одним индексом n : так, а + n обозначает оператор рождения частицы в состоянии с набором квантовых чисел n . Средние числа частиц, находящихся в состояниях, соответствующих различным n , называются числами заполнения этих состояний.

Рассмотрим выражение a – n а + mY 0 . Сначала на Y 0 действует «ближайший» к нему оператор а + m ; это отвечает порождению частицы в состоянии m . Если n = m , то последующее действие оператора а – n приводит опять к Y 0 , т. е. а – n а + n Y 0= Y 0 . Если n ¹ m , то а – n а + m Y 0= 0 , поскольку невозможно уничтожение таких частиц, которых нет (оператор а – n описывает уничтожение частиц в таких состояниях n , каких не возникает при действии a + nна Y 0 ). С учетом различных состоянии частиц перестановочные соотношения для операторов рождения и уничтожения имеют следующий вид:

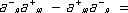
а – nа – m—а – mа – n= 0 ,

а + nа + m—а + mа + n= 0 (7)

Однако существуют поля, для которых связь между произведением операторов рождения и уничтожения, взятых в различном порядке, имеет др. вид: знак минус в (7) заменяется на плюс (это называется заменой коммутаторов на антикоммутаторы),

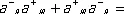
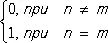(8)

а – nа – m—а – mа – n= 0 , а + nа + m—а + mа + n= 0

[эти соотношения также относят к классу перестановочных соотношений, хотя они и не имеют вида (6)]. Операторы, подчиняющиеся соотношениям (8), необходимо вводить для полей, кванты которых имеют полуцелый спин (т. е. являются фермионами ) и вследствие этого подчиняются Паули принципу , согласно которому в системе таких частиц (например, электронов) невозможно существование двух или более частиц в одинаковых состояниях (в состояниях с одинаковым набором всех квантовых чисел). Действительно, построив вектор состояния, содержащего 2 частицы (двухчастичного состояния), а + mа + nY 0 , нетрудно убедиться [учитывая (8)], что при n = m он равен самому себе с обратным знаком; но это возможно только для величины, тождественно равной нулю. Т. о., если операторы рождения и уничтожения частиц удовлетворяют перестановочным соотношениям (8), то состояния с двумя (или более) частицами, имеющими одинаковые квантовые числа, автоматически исключаются. Такие частицы подчиняются Ферми — Дирака статистике . Для полей же, кванты которых имеют целый спин, операторы рождения и уничтожения частиц удовлетворяют соотношениям (7); здесь возможны состояния с произвольным числом частиц, имеющих одинаковые квантовые числа.