БСЭ БСЭ - Большая Советская Энциклопедия (КР)

Соч.: Собр. соч., т. 1—2, СПБ, 1911.

Лит.: Ленин В. И., Что такое «друзья народа» и как они воюют против социал-демократов?, Полн. собр. соч., 5 изд., т. 1; его же, Экономическое содержание народничества и критика его в книге г. Струве, там же; Валк С. Н., С. Н. Кривенко в нелегальной литературе, в сб.: Из истории рабочего класса и революционного движения, М., 1958.

Ю. Н. Коротков.

Кривизна'(матем.), величина, характеризующая отклонение кривой (поверхности) от прямой (плоскости). Отклонение дуги MN кривой L от касательной МР в точке М можно охарактеризовать с помощью т. н. средней кривизны k cp этой дуги, равной отношению величины ее угла между касательными в точках М и N к длине D s дуги MN:

.

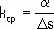Для дуги окружности средняя кривизна равна обратной величине радиуса этой окружности и, т. о., наглядно характеризует степень искривлённости окружности — с уменьшением радиуса увеличивается искривлённость дуги.

Предельное значение средней кривизны при стремлении точки N кривой к точке М, т. е. при D s ®0, называется кривизной k кривой L в точке М:

.

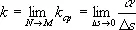Величина R, обратная кривизне, обычно называется радиусом кривизны кривой L в точке М.

Если кривая L является графиком функции у = f ( x ) , то кривизна k этой кривой может быть вычислена по формуле

.

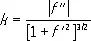Кривизна k кривой L представляет собой, вообще говоря, функцию длины дуги s , отсчитываемой от некоторой точки М этой кривой. Если для двух плоских кривых L 1 и L 2К. как функции длины дуги одинаковы, то кривые L 1и L 2 конгруэнтны — они могут быть совмещены движением. Поэтому задание К. плоской кривой как функции длины дуги обычно называется натуральным (внутренним) уравнением этой кривой.

Для характеристики отклонения пространственной кривой L от плоскости вводят понятие т. н. кручения, которое иногда называют второй К. Кручение s в точке М кривой определяется как предел отношения угла b между соприкасающимися плоскостями к кривой в точках М и N к длине D s дуги MN при стремлении точки N к М:

.

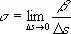При этом угол b считается положительным, если поворот соприкасающейся плоскости в N при стремлении N к М происходит против часовой стрелки при наблюдении из точки М. К. и кручение, заданные как функции длины дуги, определяют кривую L с точностью до положения в пространстве.

Исследование отклонения поверхности от плоскости может быть проведено следующим образом. Через нормаль в данной точке М поверхности проводят всевозможные плоскости. Сечения поверхности этими плоскостями называют нормальными сечениями, а кривизны нормальных сечений в точке М — нормальными кривизнами поверхности в этой точке. Максимальная и минимальная из нормальных кривизн в данной точке М именуются главными кривизнами. Если k 1 и к 2— главные кривизны, то величины K=k 1×k 2 и Н = 1/ 2 ( k 1 + k 2) называют соответственно полной кривизной (или гауссовой кривизной) и средней кривизной поверхности в точке М. Эти К. поверхности определяют нормальные К., поэтому могут служить характеристикой отклонения поверхности от плоскости. В частности, если К = 0 и Н = 0 во всех точках поверхности, то поверхность представляет собой плоскость.

Полная К. не меняется при изгибаниях поверхности (деформациях поверхности, не меняющих длин линий на ней). Если, например, полная К. равна нулю во всех точках поверхности, то каждый достаточно малый её кусок может быть изогнут на плоскость. Полная К. на поверхности без обращения к объемлющему пространству составляет объект т. н. внутренней геометрии поверхности. Средняя К. связана с внешней формой поверхности.

Понятие К. обобщается на объекты более общей природы. Например, понятие К. возникает в т. н. римановых пространствах , представляя собой меру отклонения этих пространств от евклидовых.

Лит.: Бляшке В., Дифференциальная геометрия и геометрические основы теории относительности Эйнштейна, пер. с нем., т.1, М.— Л., 1935; Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969.

Э. Г. Позняк.

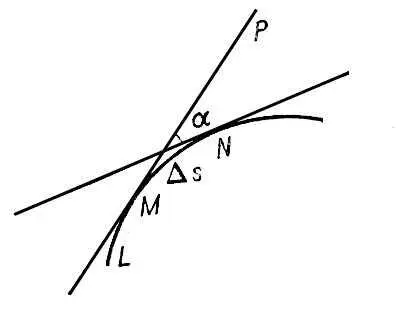
Рис. к ст. Кривизна.

Кривизна' по'ляизображения, одна из аберраций оптических систем ; заключается в том, что изображение плоского предмета получается резким не в плоскости, как это должно быть в идеальной системе, а на искривленной поверхности. Если линзы, входящие в состав центрированной системы, имеют сферические преломляющие поверхности радиусов r k ( k — номер поверхности по ходу светового луча) и, кроме того, в системе исправлен астигматизм, то изображение плоскости, перпендикулярной оси системы, представляет собой сферу. Её радиус R определяется соотношением

,

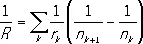где n k, n k+1— показатели преломления сред, расположенных перед и за k- той преломляющей поверхностью. В случае, когда линзы в системе можно считать тонкими (см. Линза ) , (*) сводится к более простой формуле: 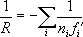, где f’ i - фокусное расстояние i- той линзы, n i— показатель преломления её материала. В сложных оптических системах (например, в фотографических объективах ) К. п. исправляют, сочетая линзы с поверхностями разной кривизны так, чтобы правая часть формулы (*) стала равна нулю (т. н. условие Пецваля).

Лит.: Тудоровский Д. И., Теория оптических приборов, 2 изд., М.— Л., 1948; Слюсарев Г. Г., Методы расчёта оптических систем, 2 изд., Л., 1969,

Кривизна' простра'нства-време'ни,в общей теории относительности (теории тяготения ) величина, характеризующая меру отклонения свойств пространства-времени от свойств так называемого плоского пространства-времени специальной теории относительности. Понятие К. н.-в. возникло по аналогии с понятием полной кривизны в геометрии поверхностей. К. п.-в. описывается тензором кривизны (см. Римановы геометрии ) . От вида тензора К. п.-в. существенно зависит тип космологических моделей (см. Космология ) .