БСЭ БСЭ - Большая Советская Энциклопедия (КР)

К. Р. возник из почтовой станции, основанной 27 апреля 1775 в урочище Кривой Рог. С 20-х гг. 19 в. К. Р. — военное поселение; с 1860 — местечко. Начало промышленного развития связано с добычей железной руды (80-е гг. 19 в.) и постройкой железной дороги, связавшей Криворожский бассейн с Донбассом. Большинство рудников К. Р. принадлежало иностранным (главным образом французам) капиталистам, часть которых в 1907 объединилась в синдикат «Продаруд». Первые с.-д. кружки в К. Р. возникли в начале 1903. Советская власть в городе была установлена 9(22) января 1918 и окончательно упрочена в 1920. С 14 августа 1941 по 22 февраля 1944 К. Р. был оккупирован немецко-фашистскими войсками, которые нанесли городу крупный ущерб. В послевоенные годы К. Р. восстановлен и является крупным индустриальным и культурным центром Украины. К. Р. — центр Криворожского железорудного бассейна. В К. Р. — мощные шахты, оборудованные новейшей техникой (среди них — «Гигант-Глубокая», им. В. И. Ленина, Гвардейская и др.). Большое развитие получила металлургическая ( Криворожский металлургический завод им. В. И. Ленина; горнообогатительные комбинаты — Северный, Центральный, Южный, Новокриворожский, Ингулецкий), машиностроительный и металлообрабатывающий (завод горного оборудования «Коммунист»), энергетическая, коксохимическая промышленность. Выросла промышленность стройматериалов (цементный, кирпичные заводы); заводы крупнопанельного домостроения. Предприятия лёгкой (обувная фабрика), пищевой и деревообрабатывающей промышленности. В 1970 жилой фонд города составил свыше 5 млн. м 2 (против 833 тыс. м 2 в 1940). Имеются горнорудный, педагогический институты, вечерний факультет Днепропетровского металлургического института, филиал Донецкого института советской торговли, 15 техникумов (в т. ч. рудничной автоматики, политехнический, горной электромеханики, металлургический, коксохимический, горно-механический и др.); авиационное училище специальных служб гражданской авиации, медицинское, музыкальное училища. Русский музыкально-драматический театр им. Т. Г. Шевченко, цирк. Историко-краеведческий музей. Среди отдельных зданий и комплексов послевоенного периода: Русский музыкально-драматический театр им. Т. Г. Шевченко (1949—50, архитектор В. А. Зуев), Дворец культуры металлургов (1952—54, архитектор К. С. Барташевич), здание Горнорудного института (1960—64), цирк (1968—69, архитектор Г. В. Наприенко, С. М. Гельфер), шахта «Родина» (1972, архитектор Е. Г. Пестрякова, инженер В. А. Бондаренко и др.), здание института «Гипрорудмаш» (1972, архитектор Д. А. Лившиц). Город награжден орденом Ленина (1971).

Лит.: Ленин В. И., Полн. собр. соч., 5 изд., т. 3, с. 238; Пахомов А., Борьба трудящихся Криворожья за власть Советов, Днепропетровск, 1958; Криворожье. Справочник-путеводитель, Днепропетровск, 1963; Варгатюк П. Л., Криворiжжя. Путiвник, Днiпропетровськ, 1969.

П. Л. Варгатюк, О. А. Савельев.

Криволе'сье,лес из невысоких деревьев и кустарников с искривленными стелющимися по склонам гор стволами и поднимающимися вверх ветвями. Развитие К. связано с сильными ветрами и обильными снегопадами; деревья перезимовывают под снегом в пригнутом состоянии, а весной после таяния снега их ветви выпрямляются ( рис. ). К. часто образует труднопроходимые заросли высотой 3—4 м. Встречается на С., близ границы существования лесов (лесотундра) и в субальпийском горном поясе. В Альпах и на Балканах образованы горной сосной (сосновым стлаником), на Камчатке — кедровым стлаником и ольховником. Очень разнообразны К. на Кавказе — буковые, берёзовые (из берёзы Медведева, берёзы Литвинова), из понтийского дуба. Субальпийские К. играют большую роль в режиме многих рек, имеют водоохранное и почвозащитное значение.

Кроны деревьев криволесья (кедровник), освобождающиеся весной из-под снега (Камчатка).

Криволине'йные координа'ты,см. Координаты.

Криволине'йный интегра'л,интеграл, взятый вдоль какой-либо кривой на плоскости или в пространстве. Различают К. и. 1-го и 2-го типов. К. и. 1-го типа возникает, например, при рассмотрении задачи о вычислении массы кривой переменной плотности; он обозначается через

,

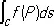где С — заданная кривая, ds — дифференциал её дуги, a f ( P ) — функция точки на кривой, и представляет собой предел соответствующих интегральных сумм (см. Интеграл ) . В случае плоской кривой С , заданной уравнением у = у ( х ) , К. и. 1-го типа сводится к обыкновенному интегралу по формуле:

.

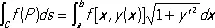К. и. 2-го типа возникает, например, при рассмотрении задачи о работе силового поля; в случае плоской кривой С он имеет вид:

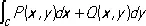
и является также пределом соответствующих интегральных сумм. К. и. 2-го типа сводится к обыкновенному интегралу по формуле:

,

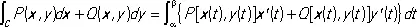где х = x ( t ) , у = у ( t ) (a £ t £ b) — уравнения кривой С в параметрической форме, и к К. и. 1-го типа по формуле:

;

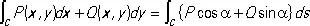здесь a — угол между осью Ox и касательной к кривой, направленной в сторону возрастания дуги.

Аналогично определяется К. и. 2-го типа в пространстве. О К. и. 2-го типа с векторной точки зрения см. Векторное исчисление.

Пусть D — некоторая область и С — её граница. При некоторых условиях между К. и. по кривой С и двойным интегралом по области D (см. Кратный интеграл ) имеет место соотношение:

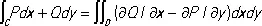
(см. Грина формулы ) , а между К. и. и поверхностным интегралом— соотношение:

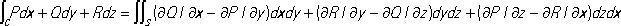
(см. Стокса формула ) .

Особенно большое значение К. и. приобрели в теории функций комплексного переменного (см. Аналитические функции ) . К. и. имеют широкое применение в различных областях механики, физики и техники.