БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

Г. Ю. Филановский.

Лине'йная а'лгебра, наиболее важная в приложениях часть алгебры. Первым по времени возникновения вопросом, относящимся к Л. а., была теория линейных уравнений. Развитие последней привело к созданию теории определителей, а затем теории матриц и связанной с ней теории векторных пространств и линейных преобразований в них. В Л. а. входит также теория форм, в частности квадратичных форм, и частично теория инвариантов и тензорное исчисление. Некоторые разделы функционального анализа представляют собой дальнейшее развитие соответствующих вопросов Л. а., связанное с переходом от n -мерных векторных пространств к бесконечномерным линейным пространствам.

Лит.: Александров П. С., Лекции по аналитической геометрии..., М., 1968; Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968; Мальцев А. И., Основы линейной алгебры, 3 изд., М., 1970; Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд., М. — Л., 1963.

Лине'йная ве'ктор-фу'нкция, функция f ( x ) векторного переменного х , обладающая следующими свойствами: 1) f ( x + у ) = f ( x ) + f ( y ) , 2) f (l x ) = l f ( x ) (l — число). Л. в.-ф. в n -мерном пространстве вполне определяется значениями, принимаемыми ею для n линейно независимых векторов. Скалярную (принимающую числовые значения) Л. в.-ф. называют также линейным функционалом; в n-mepном пространстве она выражается линейной формой, f ( x ) = a 1x 1+ a 2x 2+... + a nx n от координат x 1, x 2,..., x n вектора х . Примером скалярной Л. в.-ф. является скалярное произведение вектора х и некоторого постоянного вектора а :

f ( x ) = ( а, х ) ,

в пространстве, в котором определено скалярное произведение, всякая скалярная Л. в.-ф. имеет такой вид. Векторная (принимающая векторные значения) Л. в.-ф. определяет линейное или аффинное преобразование пространства и называется также линейным оператором, или аффинором. Векторная Л. в.-ф. у = f ( x ) в n -мерном пространстве выражается в координатах формулами:

y 1= a 11x 1+ a 12x 2+ ... + a 1nx n,

y 2= a 21x 1+ a 22x 2+ ... + a 2nx n,

...

y n= a n1x 1+ a n2x 2+ ... + a nnx n.

Здесь числа a ij ( i, j = 1, 2,..., n ) составляют матрицу векторной Л. в.-ф. Если определить сумму векторных Л. в.-ф. f ( x ) и g ( x ) как Л. в.-ф. f ( x ) + g ( x ) , а произведение тех же функций, как Л. в.-ф. g{f ( x ) }, то сумме и произведению векторных Л. в.-ф. будут соответствовать сумма и произведение соответствующих матриц. Примером векторной Л. в.-ф. является Л. в.-ф. вида:

f ( x ) = ( A 1, х ) a 1+ ( А 2, х ) a 2+... + ( A n, х ) a n,

где A 1 , A 2 , ..., A n , a 1 , a 2 , ... a n — постоянные векторы; в n-мерном пространстве, в котором определено скалярное произведение, всякая векторная Л. в.-ф. может быть представлена в таком виде.

Функцию нескольких векторных переменных, являющуюся Л. в.-ф. относительно каждого своего аргумента, называют полилинейной (билинейной, трилинейной и т. д.) вектор-функцией. Скалярное и векторное произведения двух переменных векторов могут служить примерами, соответственно скалярной и векторной билинейных вектор-функций. Полилинейные вектор-функции приводят к понятию тензора. О Л. в.-ф. (линейных функционалах и операторах) в бесконечномерном пространстве см. Функциональный анализ.

Лине'йная зави'симость(матем.), соотношение вида

C 11u 1+ C 2u 2+ ... + C nu n = 0, (*)

где С 1, C 2, ..., C n — числа, из которых хотя бы одно отлично от нуля, а u 1, u 2, ..., u n — те или иные матем. объекты, для которых определены операции сложения и умножения на число. В соотношение (*) объекты u 1, u 2, ..., u n входят в 1-й степени, т. е. линейно; поэтому описываемая этим соотношением зависимость между ними называется линейной. Знак равенства в формуле (*) может иметь различный смысл и в каждом конкретном случае должен быть разъяснён. Понятие Л. з. употребляется во многих разделах математики. Так, можно говорить о Л. з. между векторами, между функциями от одного или нескольких переменных, между элементами линейного пространства и т. д. Если между объектами u 1, u 2, ..., u n имеется Л. з., то говорят, что эти объекты линейно зависимы; в противном случае их называется линейно независимыми. Если объекты u 1, u 2, ..., u n линейно зависимы, то хотя бы один из них является линейной комбинацией остальных, т. е.

u 1= a 1u 1+ ... + a i-1u i-1+ a i+1u i+1+ ... + a nu n.

Непрерывные функции от одного переменного

u 1= j 1 ( х ) , u 2= j 2 ( х ) , ..., u n= j n ( x ) называются линейно зависимыми, если между ними имеется соотношение вида (*), в котором знак равенства понимается как тождество относительно х . Для того чтобы функции j 1 ( x ) , j 2 ( x ) , ..., j n ( x ) , заданные на некотором отрезке а £ х £ b, были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль их определитель Грама

где

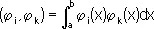
i, k = 1,2, ..., n .

Если же функции j 1(x), j 2(x), ..., j n(x) являются решениями линейного дифференциального уравнения, то для существования Л. з. между ними необходимо и достаточно, чтобы вронскиан обращался в нуль хотя бы в одной точке.

Линейные формы от m переменных

u 1= a i1x 1+ a i2x 2+ ... + a imx m

( i = 1, 2, ..., n )

называются линейно зависимыми, если существует соотношение вида (*), в котором знак равенства понимается как тождество относительно всех переменных x 1, x 2, ..., x m . Для того чтобы n линейных форм от n переменных были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль определитель

D=

Лине'йная подстано'вка, замена переменных x 1, x 2,..., x m переменными y 1, y 2, ..., y n по формулам

x 1= a i1y 1+ a i2y 2+ ... + a iny n,

i = 1,2, ..., m ,

a ij — постоянные. Линейные преобразования и переход от одной системы координат к другой в векторном пространстве осуществляются Л. п.

Лине'йная поляриза'ция, состояние распространяющейся электромагнитной волны (например, световой), при котором её электрический вектор Е в каждой точке пространства, занятого волной, совершая колебания, остаётся всё время в одной и той же плоскости, проходящей через направление распространения волны (то же справедливо и по отношению к магнитному вектору волны Н). См. Поляризация света.