БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

Лине'йная систе'мав музыке, система параллельных горизонтальных линий для записи нот; см. Нотное письмо.

Лине'йная та'ктика, теория и практика подготовки и ведения боя в линейных боевых порядках при равномерном распределении войск (сил флота) по фронту, существовавшая в 17—18 вв. Получила развитие в связи с оснащением армий огнестрельным оружием и повышением роли огня в бою. Войска для ведения боя располагались в линию, состоявшую из нескольких шеренг (их количество определялось в зависимости от скорострельности оружия), что позволяло одновременно вести огонь из наибольшего количества ружей. Тактика войск сводилась в основном к фронтальному столкновению. Исход сражения во многом решался мощью пехотного огня.

Л. т. в Западной Европе зародилась в конце 16 — начале 17 вв. в нидерландской пехоте, где квадратные колонны были заменены линейными построениями. В русских войсках элементы Л. т. впервые были применены в сражении при Добрыничах (1605). Полное оформление Л. т. получила в шведской армии Густава II Адольфа в период Тридцатилетней войны 1618—1648, а затем была принята во всех европейских армиях. Этому способствовало увеличение скорострельности мушкета и усовершенствование артиллерии. Густав II Адольф увеличил число мушкетёров до 2/ 3состава своей пехоты, полностью отказался от глубоких построений и перешёл к строю в 6 и менее шеренг. Превосходство линейного боевого порядка над старым боевым порядком из колонн окончательно определилось в сражениях при Брейтенфельде (1631) и Лютцене (1632), но одновременно выявились и отрицательные стороны Л. т.: невозможность сосредоточения превосходящих сил на решающем участке боя, способность действовать только на открытой равнинной местности, слабость флангов и трудность осуществления маневра пехоты, в силу чего решающее значение для исхода боя приобрела кавалерия. Наёмные солдаты удерживались в сомкнутых линиях с помощью палочной дисциплины, а при нарушении строя убегали с поля боя. Классические формы Л. т. получила в 18 в., особенно в прусской армии Фридриха II, который жесточайшей муштрой довёл боевую скорострельность каждой линии до 2—3 залпов в минуту. Чтобы устранить недостатки Л. т., Фридрих II ввёл косой боевой порядок (батальоны наступали уступом), состоявший из 3 линий батальонов, имевших по 3 шеренги. Конница строилась в 3 линии. Артиллерия размещалась в интервалах между батальонами, на флангах и впереди боевого порядка. Несмотря на достигнутое совершенство, Л. т. войск Фридриха II продолжала оставаться шаблонной и негибкой. Русские полководцы 18 в. — Петр I, П. С. Салтыков, П. А. Румянцев, А. В. Суворов, придерживаясь Л. т., искали новые способы ведения боя. Петр I в линейном боевом порядке создавал резерв, Румянцев начал применять рассыпной строй и каре. Суворов наряду с линейным боевым порядком ввёл колонны, применял каре, рассыпной строй и сочетание всех этих форм боевого построения войск. К концу 18 в. Л. т. исчерпала свои возможности, французская, русская, затем и др. армии перешли к новой тактике, основанной на сочетании колонн и рассыпного строя. (См. Военное искусство. )

Л. т. до конца 18 в. господствовала также и в ВМФ. Корабли для ведения морского боя строились в линию, исход боя решался фронтальным столкновением и одновременным ведением огня из орудий большинства кораблей. В конце 18 в. в ВМФ перешли к новой — манёвренной тактике, основы которой были заложены русскими адмиралами Г. А. Спиридовым и Ф. Ф. Ушаковым. (См. Военно-морское искусство. ) В современных условиях термин «Л. т.» обычно употребляется, когда имеются в виду неповоротливые боевые порядки, отсутствие их глубины, равномерное распределение сил по фронту, неспособность к маневру с изменением обстановки и др.

И. И. Картавцев.

Лине'йная фо'рма, форма первой степени. Общий вид Л. ф. n переменных x 1, x 2, ..., x n :

f ( x 1, x 2, ..., x n ) = a 1x 1+a 2x 2+ ... + a nx n ,

где a 1, а 2, ..., a n — постоянные. Если x 1, x 2, ..., x n трактовать как координаты вектора х в n -мерном векторном пространстве, то f удовлетворяет условию

f (a x + b у ) = a f ( x ) + b f ( y )

(где х , у — векторы, a , b — числа), которое может быть принято за определение.

Лине'йная фу'нкция, функция вида у = kx + b . Основное свойство Л. ф.: приращение функции пропорционально приращению аргумента. Графически Л. ф. изображается прямой линией. При равных масштабах на осях коэффициент k ; (угловой коэффициент) равен тангенсу угла, образованного прямой с осью Ox ( k = tg j, см. рис .), а b — отрезку, отсекаемому прямой на оси Оу. При b = 0 Л. ф. называется однородной; её график изображает пропорциональную зависимость: у = kx . Л. ф. широко применяется в физике и технике для представления (нередко — приближённо) зависимостей между различными величинами. Рассматривают также Л. ф. многих переменных; однородные Л. ф. многих переменных называют линейными формами. Если и аргумент и функция суть векторы, то однородными Л. ф. являются линейные преобразования.

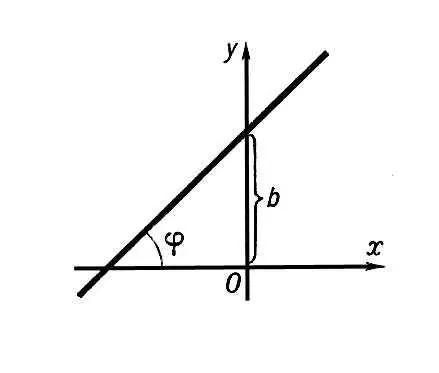
Рис. к ст. Линейная функция.

Лине'йная эро'зия, размыв горных пород и почв водой, текущей по устойчивым руслам; Л. э. приводит к образованию рытвин, оврагов, балок, долин. См. Эрозия.

Лине'йного интерполи'рования ме'тод, один из методов приближённого вычисления корней уравнения (трансцендентного или алгебраического) f ( x ) = 0 . Сущность Л. и. м. заключается в следующем. Исходя из двух близких к корню а значений x 0 и x 1 , в которых функция f ( x ) принимает значения разных знаков, берут в качестве следующего приближённого значения x 2корня a точку пересечения с осью абсцисс прямой, проходящей через точки ( x 0, f ( x 0 )) и ( x 1, f ( x 1 )) (см. рис .). Повторяя эту процедуру на более узком интервале [ х 0, x 2 ], находят следующее приближение x 3 и т. д. Общая формула Л. и. м. имеет вид

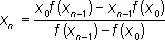, ( n = 2, 3, ...).

Др. названия Л. и. м.: метод хорд, метод секущих и (устаревшее) правило ложного положения (Regula faisi).

Лит.: Березин И. С.. Жидков Н. П., Методы вычислений, 2 изд., т. 2, М., 1962.