БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

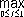
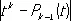
имел наименьшее значение. Вводя в пространство С[0,1] норму формулой

=

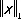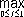
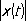
эту задачу можно сформулировать следующим образом: требуется найти многочлен P k -i ( t ), расстояние которого от функции t* было бы наименьшим. При рассмотрении же многочленов, ортогональных с весом p(t) (см. Ортогональная система функций ) , естественно рассматривать норму, определённую формулой

,

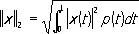и решать задачу о наилучшем приближении в смысле этой нормы. Нормы 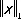и 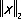существенно различны, так как, например, последовательность функций

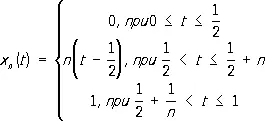
по первой норме расходится, а по второй норме при p ( t ) = 1 сходится к функции

.

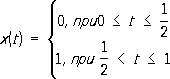Следует отметить, что хотя все функции x n ( t ) были непрерывны, функция x ( t ) разрывна. Это связано с тем, что пространство непрерывных функций неполно относительно нормы 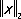. При этом нормированное Л. п. называется полным, если для любой последовательности { x n} его элементов, удовлетворяющих условию

,

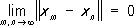существует в Л. п. такой элемент х, что данная последовательность сходится к нему, т. е.

,

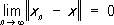Если Л. п. неполно, то к нему можно присоединить новые элементы (пополнить его) так, что оно станет полным. Например, пополняя пространство непрерывных функций, взятое с нормой 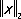, получают гильбертово пространство L 2 p. Полные нормированные Л. п. называется банаховыми, или В-пространствами, — по имени изучившего их основные свойства С. Банаха.

Обобщением понятия B -пространства является понятие топологического Л. п. Так, называют множество Е, если: 1) оно представляет собой Л. п., 2) оно является топологическим пространством, 3) операции сложения и умножения на числа в Е непрерывны относительно заданной в Е топологии. К числу топологического Л. п. относятся все нормированные пространства. А. Н. Колмогоров установил (1934) необходимые и достаточные условия нормируемости топологического Л. п.

Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965.

Лине'йное судохо'дство, см. Морские линии.

Лине'йное уравне'ние, уравнение, в которое неизвестные входят в 1-й степени (т. е. линейно) и отсутствуют члены, содержащие произведения неизвестных. Несколько Л. у. относительно одних и тех же неизвестных образуют систему Л. у. Решением системы Л. у. называют набор чисел c 1, c 2, ..., c n , обращающих все уравнения в тождества после подстановки их вместо соответствующих неизвестных. Система Л. у. может иметь как одно единственное решение, так и бесконечное множество решений (неопределённая система); может также оказаться, что система Л. у. не имеет ни одного решения (несовместная система).

Чаще всего встречается случай, когда число уравнений совпадает с числом неизвестных. Одно Л. у. с одним неизвестным имеет вид:

ax = b ;

решением его при а ¹ 0 будет число b/a. Система двух Л. у. с двумя неизвестными имеет вид:

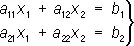(1)

где a 11, a 12, a 21, a 22, b 1, b 2 — какие-либо числа. Решение системы (1) можно получить с помощью определителей:

,

;

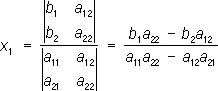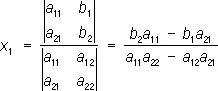здесь предполагается, что стоящий в знаменателе определитель 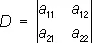отличен от нуля. В числителях стоят определители, получающиеся из D заменой в нём одного столбца столбцом свободных членов b 1, b 2 ; в выражении для первого неизвестного x 1 заменяется первый столбец, а в выражении для второго неизвестного x 2 — второй.

Аналогичное правило применимо и при решении любой системы и Л. у. с n неизвестными, т. е. системы вида:

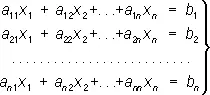(2)

здесь a ij и b i ( i, j = 1, 2, ..., n ) — произвольные числовые коэффициенты; числа b 1, b 2, ..., b n называют обычно свободными членами. Если определитель D = ½a ij½ системы (2), составленный из коэффициентов a ijпри неизвестных, отличен от нуля, то решение получается следующим образом: k -e ( k = 1, 2, ..., n ) неизвестное x k равно дроби, в знаменателе которой стоит определитель D , а в числителе — определитель, полученный из D заменой в нём столбца из коэффициентов при отыскиваемом неизвестном ( к -го столбца) столбцом свободных членов b 1, b 2, ..., b n . Если D = 0, то система (2) либо не имеет ни одного решения, либо имеет бесконечное множество решений.

Если все b i = 0 (систему Л. у. называют в этом случае однородной), то при D ¹ 0 решение системы (2) будет нулевым (т. е. все x k = 0). В практике часто, однако, встречаются однородные системы Л. у. с числом уравнений на 1 меньше числа неизвестных, т. е. системы вида:

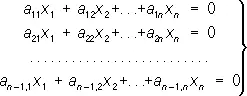(3)

Решение такой системы неоднозначно; из неё, как правило, можно найти только отношение неизвестных:

x 1: x 2: ... : x n= D 1: D 2: ... : D n,

где D n — умноженный на ( — 1) kопределитель, полученный из матрицы коэффициентов a ijсистемы (3) вычёркиванием какого-то столбца (это правило применимо только тогда, когда хотя бы один из определителей D i отличен от 0).