БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

Лит.: Knuth I., Electrische Maschinen mit geradliniger Bewegung und ihre technische Anwendung, «Electro-Praktiker», 1969, № 1.

Ю. М. Иньков.

Лине'йный кора'бль, линкор, 1) в парусном военном флоте 17—1-й половине 19 вв. крупный по размерам трёхмачтовый боевой корабль с 2—3 артиллерийскими палубами (деками); имел от 60 до 135 орудий, устанавливавшихся по бортам в линию и до 800 человек экипажа. Вёл бой, находясь в кильватерной колонне (линии баталии), отчего и получил своё название, перешедшее по традиции к кораблям парового флота.

2) В паровом броненосном флоте один из основных классов самых крупных по размерам артиллерийских надводных кораблей, предназначенных для уничтожения в морском бою кораблей всех классов, а также нанесения мощных артиллерийских ударов по береговым объектам. Л. к. появились во многих флотах мира после русско-японской войны 1904—05 взамен броненосцев. Сначала назывались дредноутами. В России название класса Л. к. установлено в 1907. Л. к. применялись в 1-й мировой войне 1914—18. К началу 2-й мировой войны 1939—45 Л. к. имели стандартное водоизмещение от 20 до 64 тыс. т, вооружение — до 12 башенных орудий главного калибра (от 280 до 460 мм ) , до 20 орудий противоминной, зенитной или универсальной артиллерии калибра 100—127 мм, до 80—140 зенитных малокалиберных автоматических пушек и крупнокалиберных пулемётов. Скорость хода Л. к. — 20—35 узлов (37—64,8 км/ч ) , экипаж военного времени — 1500—2800 человек. Бортовая броня достигала 440 мм, вес всей брони составлял до 40% общего веса корабля. На борту Л. к. имелись 1—3 самолёта и катапульта для их взлёта. В ходе войны в связи с возрастанием роли морской, особенно авианосной авиации, а также подводных сил флота и гибелью многих Л. к. от ударов авиации и подводных лодок они утратили значение; после войны во всех флотах почти все Л. к. сданы на слом.

Б. Ф. Балев.

Линейный корабль «Айова» (США). 1943.

Лине'йный кре'йсер, подкласс крейсеров с мощным артиллерийским вооружением, появившийся перед 1-й мировой войной 1914—18. Было построено лишь несколько Л. к., имели водоизмещение от 20 до 42 тыс. т, вооружение — 6—9 башенных орудий калибра 280—380 мм, до 20 113- мм орудий, скорость хода 29—30 узлов (53,7—55,5 км/ч ) . Л. к. применялись в 1-й мировой войне, а три из оставшихся в ВМС Великобритании и во 2-й мировой войне 1939—45. После войны последний уцелевший Л. к. был сдан на слом.

Лине'йный опера'тор, обобщение понятия линейного преобразования на линейные пространства. Линейным оператором F на линейном пространстве Е называют функцию F ( x ), определённую для всех х Î Е , значения которой суть элементы линейного пространства E 1 , и обладающую свойством линейности:

F (( x + ( у ) = ( F ( x ) + ( F ( y ) ,

где х и у — любые элементы из Е , a и b — числа. Если пространства Е и E 1нормированы и величина 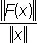ограничена, то Л. о. F называют ограниченным, а 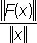его нормой.

Важнейшими конкретными примерами Л. о. в функциональных пространствах являются дифференциальные Л. о.

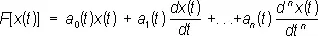
и интегральные Л. о.

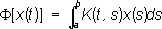
примером Л. о. функций многих переменных может служить Лапласа оператор. Теория Л. о. находит большое применение в различных вопросах математической физики и прикладной математики. См. также Функциональный анализ , Операторов теория, Спектральный анализ (математический), Собственные значения и собственные функции, Собственные векторы.

Лине'йный функциона'л, обобщение понятия линейной формы на линейные пространства. Линейным функционалом f на линейном нормированном пространстве Е называют числовую функцию f ( x ), определённую для всех х из Е и обладающую следующими свойствами:

1) f ( x ) линейна, т. е. f (( x + ( у ) = ( f ( x ) + ( f ( y ),

где х и у — любые элементы из Е , a и b — числа;

2) f ( x ) непрерывна.

Непрерывность f равносильна требованию, чтобы 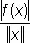было ограничено в Е ; выражение 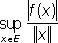называют нормой f и обозначают .

В пространстве С [ a, b ] функций a(t), непрерывных при a ( t ( b , с нормой 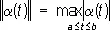Л. ф. являются, например, выражения:

,

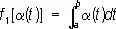f 2[ (( t ) ] = (( t 0 ) , a ( t 0 ( b.

В гильбертовом пространстве Н Л. ф. суть скалярные произведения ( l, х ), где l — любой фиксированный элемент пространства Н; ими исчерпываются все Л. ф. этого пространства.

Во многих задачах можно из общих соображений установить, что та или иная величина является Л. ф. Например, к Л. ф. приводит решение линейных дифференциальных уравнений с линейными краевыми условиями. Поэтому очень существенным является вопрос об общем аналитическом выражении Л. ф. в разных пространствах.

Совокупность всех Л. ф. данного пространства Е превращается в линейное нормированное пространство 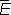, если определить естественным образом сложение Л. ф. и умножение их на числа. Пространство 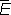называют сопряжённым к 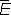; это пространство играет большую роль при изучении Е .

С понятием Л. ф. связано понятие слабой сходимости. Последовательность { xn } элементов линейного нормированного пространства называют слабо сходящейся к элементу х , если

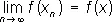
для любого Л. ф. f . См. также Функциональный анализ.