БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

Лине'йных зна'ков спо'соб, один из картографических способов изображения. Л. з. с. изображаются линии местности (например, водоразделы, тектонические разломы, линии связи, политико-административные границы и др.), объекты линейного протяжения, не выражающиеся в масштабе карты (например, реки и дороги и др.), граничные полосы (например, береговая зона, зональные границы почв и растительности и др.).

Лине'йчатая геоме'трия, раздел геометрии, в котором рассматриваются в качестве элементов пространства прямые линии. Как известно, прямая в пространстве определяется четырьмя постоянными — коэффициентами а, b, р, q в уравнениях х = az + р, у = bz + q . Следовательно, величины а, b, р, q можно рассматривать как координаты прямой. Если эти координаты являются функциями одного, двух или трёх параметров, то соответствующие совокупности прямых образуют линейчатые поверхности и т. н. конгруэнции и комплексы прямых. Эти геометрические образы и являются объектом изучения Л. г. Примером линейчатой поверхности может служить однополостный гиперболоид, примером конгруэнции — совокупность общих касательных к двум каким-либо поверхностям, примером комплекса прямых — совокупность касательных к одной какой-либо поверхности.

Для изучения линейчатых поверхностей, конгруэнций и комплексов прямых с единой точки зрения в Л. г. вводятся так называемые линейные однородные координаты прямой. Пусть заданы две точки M 1 ( x 1, y 1, z 1 ) и M 2 ( x 2, y 2, z 2 ) , тогда линейными однородными координатами прямой, проходящей через эти точки, называют шесть чисел, пропорциональных (или равных) числам:

x 1= x 1— x 2, x 2= y 1— y 2, x 3= z 1— z 2, x 4= y 1z 2— y 2z 1, x 5= x 2z 1— x 1z 2, x 6= x 1y 2— x 2y 1.

Числа x 1, x 2, x 3являются компонентами вектора 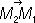, а x 4, x 5, x 6— компоненты момента этого вектора относительно начала координат. Легко проверить, что числа x iудовлетворяют соотношению

x 1x 4+ x 2x 5+ x 3x 6= 0. (1)

Таким образом, каждой прямой соответствуют шесть определяемых с точностью до постоянного множителя чисел x i, удовлетворяющих соотношению (1), и обратно, числа x i(не все равные нулю), связанные условием (1), определяют единственным образом некоторую прямую (как её координаты в указанном выше смысле). Одно однородное линейное уравнение

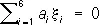(2)

определяет линейный комплекс — совокупность прямых, заполняющих пространство так, что через каждую точку пространства проходит пучок прямых, лежащих в одной плоскости. Таким образом, каждой точке («полюсу») пространства можно поставить в соответствие плоскость («полярную плоскость»), содержащую все прямые комплекса, проходящую через эту точку. Это соответствие называют нулевой системой; оно аналогично соответствию полюсов и полярных плоскостей поверхности 2-го порядка. Если полярные плоскости всех точек пространства проходят через одну прямую (ось), то комплекс состоит из всех прямых, пересекающих ось; его называют специальным линейным комплексом. В этом случае коэффициенты уравнения (2) удовлетворяют условию

a 1a 4+ a 2a 5+ a 3a 6 = 0.

Система двух однородных линейных уравнений вида (2) определяет линейную конгруэнцию — совокупность прямых, пересекающих две данные прямые (которые могут быть и мнимыми). Три однородных линейных уравнения определяют линейчатую поверхность, являющуюся в этом случае либо однополостным гиперболоидом, либо гиперболическим параболоидом.

Линейные однородные координаты прямой были введены Ю. Плюккером в 1846. Он же подробно изучил теорию линейного комплекса. В дальнейшем Л. г. разрабатывалась в работах Ф. Клейна и русского математика А. П. Котельникова. Дифференциальная геометрия конгруэнций, начатая Э. Куммером в 1860, получила большое развитие в трудах итальянских математиков Л. Бианки, Г. Санниа и французского математика А. Рибокура. На основе созданного в 1895 Котельниковым «винтового» исчисления советским математиком Д. Н. Зейлигером развита теория линейчатых поверхностей и конгруэнций. Проективная теория конгруэнций построена в 1927 советским математиком С. П. Финиковым.

Лит.: Зейлигер Д. Н., Комплексная линейчатая геометрия. Поверхности и конгруэнции, Л. — М., 1934; Фиников С. П., Теория поверхностей, М. — Л., 1934; его же, Проективно-дифференциальная геометрия, М. — Л.,1937; его же, Теория конгруэнций, М. — Л., 1950; Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1—2, М. — Л., 1947—48; Клейн Ф., Высшая геометрия, пер. с нем., М. — Л., 1939; Zindler К., Liniengeometrie, Bd 1—2, Lpz., 1902—06.

Э. Г. Позняк.

Лине'йчатая пове'рхность, совокупность прямых, зависящая от одного параметра; Л. п. можно описать движением прямой (образующей) по некоторой линии (направляющей). Л. п. разделяются на развёртывающиеся и косые.

Развёртывающиеся Л. п. могут быть посредством изгибания наложены на плоскость. Любая развёртывающаяся поверхность является либо цилиндром, либо конусом, либо поверхностью, состоящей из касательных к некоторой пространственной кривой (1) ( рис. 1 ). Эту кривую называют ребром возврата развёртывающейся поверхности. Плоскость P, пересекающая ребро возврата (L), образует в сечении с поверхностью кривую ABC с точкой возврата В (см. Особые точки ) . Ребро возврата является особой линией развёртывающейся поверхности, вдоль которой две её полости S 1и S 2касаются друг друга. Развёртывающиеся поверхности характеризуются также тем, что касательная плоскость к ним в различных точках одной и той же образующей неизменна. Отсюда следует, что совокупность всех касательных плоскостей развёртывающейся Л. п. представляет собой однопараметрическое семейство. Иначе говоря, развёртывающаяся Л. п. является огибающей однопараметрического семейства плоскостей.

У косой Л. п. касательные плоскости в различных точках одной и той же образующей различны. При перемещении точки касания вдоль образующей касательная плоскость вращается вокруг образующей. Полный поворот касательной плоскости, когда точка касания проходит всю образующую, равен 180°. На каждой образующей имеется такая точка, что для каждой из двух частей, на которые она делит образующую, полный поворот касательной плоскости равен 90°. Эту точку (на рис. 2 — точка О) называют центром образующей. Тангенс угла между касательными плоскостями к поверхности в центре О и какой-либо другой точке O' той же образующей пропорционален расстоянию OO'. Множитель пропорциональности называется параметром распределения Л. п. Абсолютная величина полной кривизны Л. п. достигает на данной образующей наибольшего значения в центре образующей и убывает при удалении от центра по образующей. Геометрическое место центров образующих носит название линии сжатия, или стрикционной линии. Например, у геликоида — Л. п., описываемой равномерным винтовым движением прямой вокруг некоторой оси (которую движущаяся прямая пересекает под прямым углом), — линией сжатия является ось (AB на рис. 2 ). Л. п. 2-го порядка — гиперболический параболоид, однополостный гиперболоид — имеют две различные системы прямолинейных образующих (из однополостных гиперболоидов сконструирована радиомачта системы В. Г. Шухова, находящаяся в Москве на Шаболовке). Две системы прямолинейных образующих имеют только Л. п. 2-го порядка.