БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

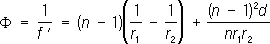(1)

Радиусы r 1и r 2считаются положительными, если направление от вершины Л. до центра соответствующей поверхности совпадает с направлением лучей (на рис. 1 r 1> 0, r 2< 0). Следует оговорить, что формула (1) верна лишь применительно к параксиальным лучам. При одной и той же оптической силе и том же материале форма Л. может быть различной. На рис. 2 показано несколько Л. одинаковой оптической силы и различной формы. Первые три — положительны, последние три — отрицательны. Л. называется тонкой, если её толщина d мала по сравнению с r 1и r 2. Достаточно точное выражение для оптической силы такой Л. получают, отбрасывая второй член в (1).

Положение главных плоскостей Л. относительно её вершин тоже можно определить, зная r 1, r 2, n и d . Расстояние между главными плоскостями мало зависит от формы и оптической силы Л. и приблизительно равно 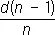. В случае тонкой Л. это расстояние мало и практически можно считать, что главные плоскости совпадают.

Когда положение кардинальных точек известно, положение изображения оптического точки, даваемого Л. ( см. рис. 1 ), определяется формулами:

x · x’ = f · f’ = -f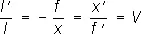’ 2,

, (2)

где V — линейное увеличение Л. (см. Увеличение оптическое ) , l и l' — расстояния от точки и её изображения до оси (положительные, если они расположены выше оси), х — расстояние от переднего фокуса до точки, x' — расстояние от заднего фокуса до изображения. Если t и t' — расстояния от главных точек до плоскостей предмета и изображения соответственно, то (т. к. х = t — f, x' = t’ — f’ ):

f’/t’ + f/t = 1 (3)

или

1/t’ - 1/t = 1/f’.

В тонких Л. t и f можно отсчитывать от соответствующих поверхностей Л.

Из (2) и (3) следует, что по мере приближения изображаемой точки (действительного источника) к фокусу Л. расстояние от изображения до Л. увеличивается; собирающая Л. даёт действительное изображение точки в тех случаях, когда эта точка расположена перед фокусом; если точка расположена между фокусом и Л., её изображение будет мнимым; рассеивающая Л. всегда даёт мнимое изображение действительной светящейся точки (подробнее см. в ст. Изображение оптическое ) .

Лит.: Элементарный учебник физики, под ред. Г. С. Ландсберга, 6 изд., т. 3, М., 1970; Тудоровский А. И., Теория оптических приборов, 2 изд., т. 1, М. — Л., 1949.

Г. Г. Слюсарев.

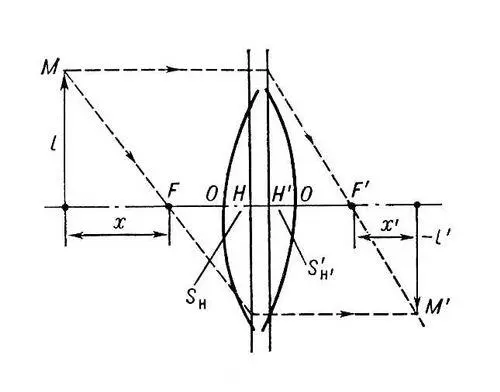
Рис. 1 к ст. Линза.

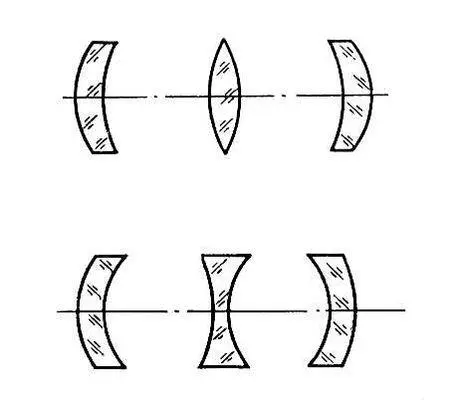
Рис. 2 к ст. Линза.

Ли'нза(геол.), форма залегания горных пород и руд в виде чечевицы с уменьшающейся к краям мощностью. Размеры Л. различны и колеблются от нескольких м длины и нескольких см мощности до 1 км и более длины и нескольких десятков м мощности. См. также Залегание горных пород.

Ли'нзовая анте'нна, антенна, диаграмма направленности которой формируется за счёт разности фазовых скоростей распространения электромагнитной волны в воздухе и в материале линзы. Л. а. применяется в радиолокационных и измерительных устройствах, работающих в диапазоне сантиметровых волн. Л. а. состоит из собственно линзы и облучателя. Форма линзы зависит от коэффициента преломления n (отношения фазовых скоростей распространения радиоволн в вакууме и линзе). При n > 1 Л. а. (как и линза в оптике) называется замедляющей, а при n < 1 — ускоряющей (последняя не имеет аналогов в оптике). В качестве облучателя Л. а. обычно используется рупорная антенна, создающая сферический фронт волны, или антенные решётки, создающие цилиндрический фронт волны.

Замедляющие Л. а. изготавливаются из высококачественных однородных диэлектрических материалов с малыми потерями (полистирол, фторопласт и др.) или из т. н. искусственных диэлектриков. Последние представляют собой систему металлических частиц различной формы, расположенных в воздухе или в однородном диэлектрике с относительной диэлектрической проницаемостью, близкой к единице. Коэффициент преломления таких искусственных диэлектриков может изменяться в широких пределах при весьма малых потерях. Ускоряющие Л. а. выполняются из металлических пластин определённой формы и не имеют аналогов в оптике. Их принцип действия объясняется зависимостью фазовой скорости электромагнитной волны, распространяющейся между параллельными металлическими пластинами, от расстояния между ними, если вектор её электрического поля параллелен пластинам. В этом случае фазовая скорость больше скорости света и коэффициент преломления меньше единицы. Для уменьшения массы и объёма Л. а. применяется зонирование её поверхностей, позволяющее также значительно уменьшить толщину Л. а. Форма и высота профилей отдельных участков (зон) линзы выбираются так, чтобы электромагнитные волны, преломленные соседними зонами линзы, выходили из неё со сдвигом фаз 360 °; в этом случае поле в раскрыве Л. а. остаётся синфазным.

В апланатических Л. а. и Люнеберга линзе возможно управление диаграммой направленности (сканирование) без существ. искажения формы диаграммы направленности.

О. Н. Терешин, Г. К. Галимов.

Ли'нзовый телеско'п, астрономический оптический инструмент, в котором изображение небесных светил строится линзовым объективом; то же, что рефрактор.

Ли'нии второ'го поря'дка, плоские линии, декартовы прямоугольные координаты которых удовлетворяют алгебраическому уравнению 2-й степени

a 11x 2+ a 12xy + a 22y 2+ 2a 13x + 2a 23y + a 11 = 0. (*)

Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий. Именно,

нераспадающиеся линии:

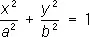— эллипсы,