БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

Ю. С. Демин, Е. Я. Борисенко.

Ли'ния(от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно.

1) В элементарной геометрии рассматриваются прямые Л., отрезки прямых, ломаные Л., составленные из отрезков, и некоторые кривые Л. Каждый вид кривых Л. определяется тем или иным специальным способом (например, окружность определяется как геометрическое место точек, имеющих заданное расстояние R от заданной точки О — центра окружности). Иногда в учебниках дают определение Л. как границы куска поверхности (поверхность определяется при этом как граница тела) или как траектории движущейся точки. Но в рамках элементарной геометрии эти определения не получают отчётливой формулировки.

2) Представление о Л. как траектории движущейся точки может быть сделано вполне строгим при помощи идеи параметрического представления Л. Например, вводя на плоскости прямоугольные координаты ( x, у ), можно параметрически задать окружность радиуса R с центром в начале координат уравнениями

x = R cos t, y = R sin t.

Когда параметр t пробегает отрезок 0 £ t £ 2p, точка ( х, у ) описывает окружность. Вообще, Л. на плоскости задают параметрическими уравнениями вида

x = j ( t ) , у = 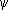( t ) ,

где j ( t ) , 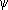( t ) — произвольные функции, непрерывные на каком-нибудь конечном или бесконечном интервале D числовой оси t . С каждым значением параметра t (из интервала D) уравнения (*) сопоставляют некоторую точку M, координаты которой определяются этими уравнениями. Л., заданная параметрическими уравнениями (*) есть множество точек, соответствующих всевозможным значениям t из D, при условии, что эти точки рассматриваются в определенном порядке, именно: если точка M 1 соответствует значению параметра t 1 , а точка M 2 — значению t 2, то M 1считается предшествующей M 2 , если t 1< t 2 При этом точки, отвечающие различным значениям параметра, всегда считаются различными.

Аналогично, в трёхмерном пространстве Л. задаётся параметрически тремя уравнениями вида

x = j ( t ) , у = 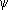( t ) , z = c ( t ) ,

где j ( t ) , 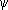( t ) , c ( t ) — произвольные функции, непрерывные на каком-нибудь интервале. В произвольном топологическом пространстве Т (которое, в частности, может быть плоскостью, поверхностью, обычным трёхмерным пространством, функциональным пространством и т. п.) Л. параметрически задают уравнением вида

P = j ( t ) ,

где j — функция действительного переменного t , непрерывная на каком-либо интервале, значения которой суть точки пространства Т. Считают, что два параметрических представления задают одну и ту же Л., если они определяют один и тот же порядок следования её точек (в смысле, указанном выше).

В анализе и топологии рассматривают обычно случай, когда область изменения параметра t есть отрезок а £ t £ b . В этом случае условие того, чтобы два параметрических представления

Р = j ( t ) , a £ t £ b

P = j 1 ( t 1 ) , a 1 £ t 1 £ b 1,

изображали одну и ту же Л., заключается в существовании непрерывной и строго возрастающей функции

t 1= f ( t ) ,

для которой

f ( a ) = a 1, f ( b ) = b 1, j ( t ) = j 1[f ( t ) ].

Такое понимание термина «Л.» наиболее естественно в большинстве вопросов анализа (например, в теории криволинейных интегралов) и механики. Так как Л. здесь рассматривается вместе с порядком, в котором пробегает её точки переменная точка М при возрастании t , то при этом естественно возникает вопрос о числе прохождений переменной точки Л. через какую-либо точку пространства. Кроме простых точек, проходимых один раз, Л. может иметь кратные точки, которые проходятся несколько раз (отвечающие различным значениям параметра).

Например, при изменении t в пределах — ¥ < t < ¥ точка с координатами

,

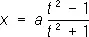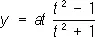
описывает строфоиду (см. рис. «Алгебраические кривые третьего порядка», № 5 ), попадая в положение х = 0, у = 0 два раза при t = — 1 и t = + 1.

3) Из аналитической геометрии известен и другой способ задания Л. на плоскости уравнением

F ( x, y ) = 0;

в пространстве — двумя уравнениями

F ( x, у, z ) = 0, G ( x, y, z ) = 0.

Ограничиваясь случаем плоскости, укажем лишь, как строится понятие алгебраической Л. (кривой) — Л., определяемой уравнением

F ( x, y ) = 0,

где F ( x, у ) — целая алгебраическая функция, т. е. многочлен како-либо степени n ³ 1. В этом случае считают, что два многочлена F 1 ( x, у ) и F 2 ( x, у ) определяют одну и ту же алгебраическую Л. в том и только в том случае, когда существует такая постоянная с ¹ 0, что выполняется тождественно соотношение

F 1 ( x, y ) = cF 2 ( x, у ) .

Таким образом, все многочлены, определяющие одну и ту же Л., имеют одну и ту же степень n , называемую порядком соответствующей Л. Например, в аналитической геометрии принято считать, что уравнение

( х - у ) 2 = 0

определяет Л. второго порядка, а именно, дважды взятую прямую х — у = 0.

В связи с последним примером необходимо заметить, однако, что часто целесообразно ограничиваться рассмотрением неприводимых алгебраических Л., т. е. таких Л., для которых многочлен не допускает представления F = GH, где G и Н — отличные от постоянных многочлены. Далее, в пункте 4, имеется в виду только этот случай.

Говорят, что точка ( x 0, y 0 ) кривой F ( x, у ) = 0 имеет кратность m, если разложение F ( x, у ) по степеням x = х — x 0 , h = у — y 0 начинается с членов степени m (по совокупности переменных x и h). В случае m = 2, т. е. в случае двойной точки

F ( x, у ) = а 11 ( х — x 0 ) 2+ 2а 12 ( х — x 0 ) ( у — y 0 ) + a 22 ( y — y 0 ) 2+ ...,

где многоточие означает, что далее следуют члены высших порядков. При помощи дискриминанта

d = a 11a 22— а 12 2

можно определить тип двойной точки (см. Особые точки ) .