БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

Циклоида (от греч. kykloeides — кругообразный) (см. рис. «Трансцендентные кривые», № 4 ), кривая, которую описывает точка Р, расположенная на расстоянии а от центра круга радиуса r , катящегося без скольжения по прямой линии. Если Р лежит на окружности круга ( r = а ), получают обыкновенную циклоиду (см. рис. «Трансцендентные кривые», № 4а ), если она лежит внутри круга ( r > а ), — укороченную циклоиду (см. рис. «Трансцендентные кривые», № 4б ), если точка вне круга ( r < а ), — удлинённую циклоиду (см. рис. «Трансцендентные кривые», № 4в ). Две последние Л. называют трохоидами. Уравнение в параметрической форме:

, .

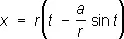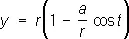Среди трансцендентных Л. особый класс составляют спирали (от греч. spéira, буквально — витое), плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или с каждым обходом удаляясь от неё. Если выбрать эту точку за полюс системы координат, то полярное уравнение спирали r = f(j) таково, что f(j + 2p) > f(j) или f(j + 2p) < f(j) при всех j. Из спиралей наиболее известны:

Архимедова спираль (см. рис. «Трансцендентные кривые», № 5 ), кривая, описываемая точкой, равномерно движущейся по прямой в то время, как эта прямая равномерно вращается в плоскости вокруг точки О. уравнение в полярных координатах: r = a j, где а — постоянная. Эта спираль изучалась Архимедом (3 в. до н. э.) в связи с задачами трисекции угла и квадратуры круга.

Гиперболическая спираль (см. рис. «Трансцендентные кривые», № 6 ), кривая, описываемая точкой М, движущейся по вращающейся прямой OA, так, что её расстояние от центра вращения меняется обратно пропорционально углу поворота. Уравнение в полярных координатах: r = а/j.

Жезл (см. рис. «Трансцендентные кривые», № 7 ), кривая, уравнение которой в полярных координатах: 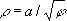. Каждому значению j соответствуют два значения r — положительное и отрицательное. Кривая состоит из двух ветвей, каждая из которых асимптотически приближается к полюсу.

Логарифмическая спираль (см. рис. «Трансцендентные кривые», № 8 ), кривая, уравнение которой в полярных координатах: r = ае к j. Была известна многим математикам 17 в.

Спираль Корню (см. рис. «Трансцендентные кривые», № 9 ), клотоида, кривая, состоящая из двух ветвей, симметричных относительно начала координат. уравнение в параметрической форме:

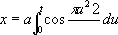, y = a .

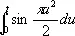Использовалась французским физиком М. А. Корню (1874) для графич. решения некоторых задач дифракции света.

Si-ci-спираль (см. рис. «Трансцендентные кривые», № 10 ), кривая, параметрическое уравнение которой имеет вид

,

,

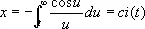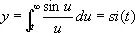si ( t ) и ci ( t ) — интегральный синус и интегральный косинус.

К циклоиде по способу построения примыкает класс циклоидальных кривых, которые могут быть как алгебраическими, так и трансцендентными. Среди них:

Гипоциклоида (см. рис. «Циклоидальные кривые», № 1а, 1б ) , кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности внутри её. Уравнение в параметрической форме:

,

,

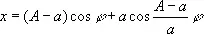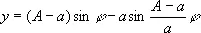где А — радиус неподвижной, а а — подвижной окружности. Вид кривой зависит от отношения А/а .

Эпициклоида (см. рис. «Циклоидальные кривые», № 2а, 2б ), кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности вне её. Уравнение получится из уравнения гипоциклоиды заменой а на — а .

Удлинённая гипоциклоида (эпициклоида), кривая, описываемая точкой, лежащей вне окружности, которая катится без скольжения по другой окружности внутри (вне) её (см. рис. «Циклоидальные кривые», № 3а, 4д ). Аналогично определяется укороченная гипоциклоида (эпициклоида) (см. рис. «Циклоидальные кривые», № 3б, 4б ). Удлинённые и укороченные гипоциклоиды и эпициклоиды иногда называются гипо- и эпитрохоидами.

В. И. Битюцков, Ю. А. Горьков, А. Б. Иванов.

Лит.: Маркушевич А. И., Замечательные кривые, 2 изд., М. — Л., 1952; Савелов А. А., Плоские кривые. Систематика, свойства, применения (Справочное руководство), М., 1960; Пархоменко А. С., Что такое линия, М., 1954; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Уокер А., Алгебраические кривые, пер. с англ., М., 1952; Loria G., Spezielle algebraische und transzendente ebene Kurven. Theorie und Geschichte, 2 Aufl., Bd 1—2, Lpz. — B., 1910—11.

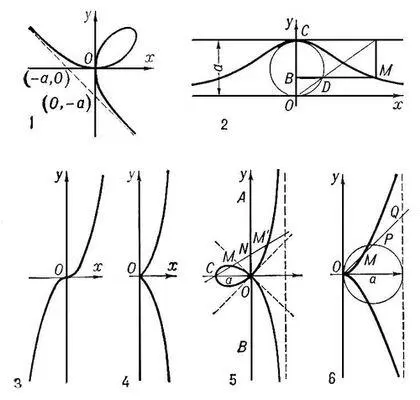
Алгебраические кривые третьего порядка: 1 — декартов лист; 2 — локон Аньези; 3 — кубическая парабола; 4 — полукубическая парабола; 5 — строфоида; 6 — циссоида Диоклеса.

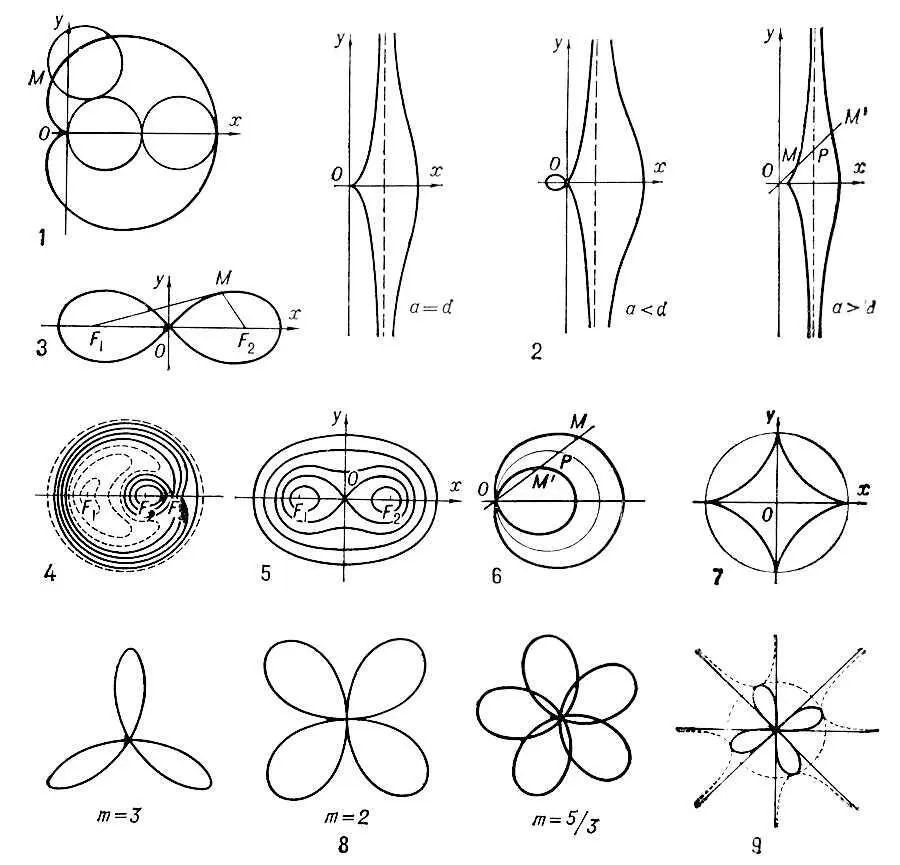
Алгебраические кривые четвёртого и более высоких порядков: 1 — кардиоида; 2 — конхоида Никомеда; 3 — лемниската Бернулли: 4 — овалы Декарта; 5 — овалы Кассини; 6 — улитка Паскаля; 7 — астроида; 8 — розы; 9 — синус-спираль.

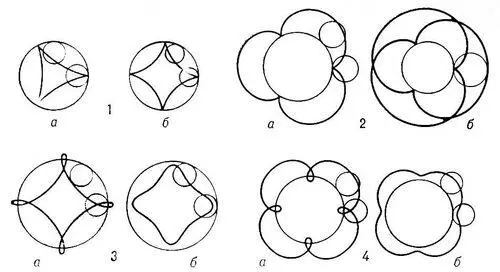
Циклоидальные кривые: 1 а, б — гипоциклоиды; 2 а, б — эпициклоиды; 3 а — удлинённая гипоциклоида; 3 б — укороченная гипоциклоида; 4а — удлинённая эпициклоида; 4б — укороченная эпициклоида.

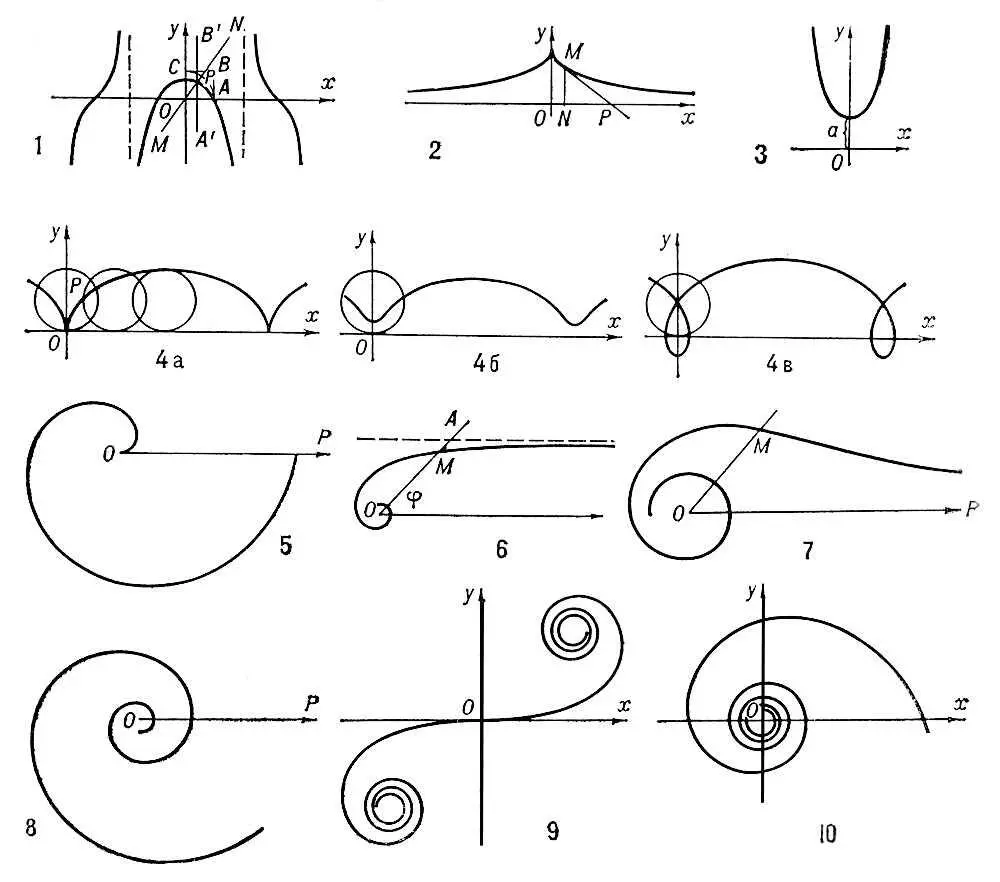
Трансцендентные кривые: 1 — квадратриса; 2 — трактриса; 3 — цепная линия; 4 — циклоида; 5 — архимедова спираль; 6 — гиперболическая спираль; 7 — жезл; 8 — логарифмическая спираль; 9 — спираль Корню; 10 — si-ci-cпираль.

Ли'ния заде'ржки, устройство, предназначенное для задержки сигналов на некоторый заданный промежуток времени. Время задержки t определяется длиной пути в Л. з. электромагнитной или звуковой волны, делённой на скорость её распространения (кроме искусственной линий с сосредоточенными постоянными). Л. з. применяют в устройствах цветного телевидения, осциллографических устройствах со ждущей развёрткой, радиолокационных станциях с селекцией подвижных целей, в устройствах оптимальной фильтрации сложных радиолокационных сигналов, в кодирующих, декодирующих и селекторных устройствах, в запоминающих устройствах и в устройствах управления ЭВМ и т. д. Л. з. изготавливаются с t от долей до десятков тысяч мксек. Они имеют один или несколько выходов с различными t (многоотводные Л. з.), t может быть постоянным либо зависеть от частоты сигнала (дисперсионные Л. з.). Разработаны также Л. з. с регулировкой t (переменные Л. з.), с подстраиваемым t (магнитоупругие Л. з.), с малым температурным коэффициентом t (термостабильные Л. з.), с внутренним усилением сигнала (активные Л. з. с фононфотонным или фонон-магнонным взаимодействием; см. Квазичастицы ) .