БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

Конхоида Никомеда (от греч. konchoeides — похожий на раковину) (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 2 ), кривая, получающаяся при увеличении или уменьшении каждого радиус-вектора точек данной прямой на одну и ту же величину d , т. о., OM = OP — d или OM' = OP + d . Если расстояние от полюса О до данной прямой равно а, то уравнение в прямоугольных координатах: ( х — а ) 2 ( х 2+ y 2 ) — d 2x 2 = 0, в полярных координатах: r = a/ cosj ± d . Впервые рассматривалась древнегреческим геометром Никомедом (около 250—150 до нашей эры), который использовал её для решения задач о трисекции угла и удвоении куба.

Лемниската Бернулли (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 3 ) (от лат. lemniscatus, буквально — украшенный лентами), кривая, имеющая форму восьмёрки; геометрическое место точек, произведение расстояний которых от фокусов F 1( — а , 0) и F 2( а , 0) равно а 2 . уравнение в прямоугольных координатах: ( x 2+ y 2 ) 2— 2a 2 ( x 2— y 2 ) =0, в полярных координатах: r 2= 2а 2cos 2j. Впервые рассматривалась Я. Бернулли (1694). Лемниската является частным случаем овалов Кассини и синус-спиралей.

Овалы Декарта (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 4 ), геометрические места точек М, расстояния которых от двух фиксированных точек F 1и F 2, называемых фокусами, умноженные на данные числа, имеют постоянную сумму с , то есть m MF 1+ + n MF 2= с . уравнение в прямоугольных координатах:

( x + y’’ —2rx ) 2— l 2 ( x 2+ y 2 ) — k = 0,

где r, l и k — некоторые постоянные, связанные с параметрами m, n и d ; в полярных координатах:

( n 2— m 2 )( 2+ 2 (( mc — n2d cos () + n 2d 2— с 2 = 0.

Помимо фокусов F 1и F 2, имеется и третий фокус F 3, равноправный с каждым из них. При m = 1, n = 1 овал Декарта превращается в эллипс; при m = 1 и n = —1 — в гиперболу. Частным случаем овала является также улитка Паскаля. Овалы впервые исследовались Р. Декартом (1637).

Овалы Кассини (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 5 ), геометрические места точек М, произведение расстояний которых от двух данных точек постоянно. Пусть F 1и F 2точки на оси абсцисс, F 1F 2= 2 b , а произведение MF 1×MF 2= а 2 . уравнение в прямоугольных координатах:

( x 2+ y 2 ) 2— 2b 2 ( a 2— y 2 ) = a 4— b 4.

Если 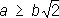, то овал Кассини — выпуклая кривая; если b < a < 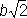, то кривая имеет вид овала с двумя утолщениями; при а = b овал Кассини превращается в лемнискату, наконец, при b > а овал Кассини является двусвязной кривой. Впервые рассмотрена Дж. Кассини (17 в.).

Улитка Паскаля (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 6 ), геометрическое место точек М и M', расположенных на прямых пучка (центр которого О лежит на окружности радиуса R) на расстоянии а по обе стороны от точки Р пересечения прямых с окружностью; т. о., PM = PM' = а . уравнение в прямоугольных координатах: ( x 2+ y 2— 2Rx ) 2— а 2 ( х 2+ y 2 ) = 0, в полярных координатах: r = 2 R cos j + а . При а = 2 R петля стягивается в точку, в этом случае улитка Паскаля превращается в кардиоиду. Название по имени французского учёного Э. Паскаля (1588—1651), впервые изучавшего её.

Астроида (от греч. ástron — звезда и éidos — вид) (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 7 ), кривая, описываемая точкой подвижной окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. уравнение в прямоугольных координатах: x 2/3+ y 2/3= а 2/3 , где а — радиус неподвижной окружности. Астроида — линия 6-го порядка.

Розы (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 8 ), кривые, полярное уравнение которых: r = a sin m j; если m — рациональное число, то розы — алгебраической Л. чётного порядка. При m нечётном роза состоит из от лепестков, при m чётном — из 2 m лепестков; при m рациональном лепестки частично покрывают друг друга.

Синусоидальные спирали, синус-спирали (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 9 ), кривые, полярное уравнение которых r m= a m cos m j; если m — рациональное число, то эти Л. — алгебраические. Частные случаи: m = 1 — окружность, m = — 1 — прямая, m = 2 — лемниската Бернулли, m = —2 — равнобочная гипербола, m = 1/ 2— кардиоида, m = — 1/ 2— парабола. При целом m > 0 Л. состоит из m лепестков, каждый из которых лежит внутри угла, равного p/ m , при рациональном m > 0 лепестки могут частично покрывать друг друга; если m < 0, то Л. состоит из от бесконечных ветвей.

Большой интересный класс составляют трансцендентные Л. К ним относятся графики тригонометрических функций (синусоида, тангенсоида), логарифмической функции, показательной функции, гиперболических функций, а также следующие Л.:

Квадратриса (см. рис. «Трансцендентные кривые», № 1 ). Пусть прямая MN равномерно вращается против часовой стрелки вокруг точки О, а прямая А'В' равномерно движется справа налево, оставаясь параллельной OC. Далее, пусть за время движения A'B' от AB до OC прямая MN поворачивается на прямой угол и переходит из положения OA = r в положение OC. Геометрическое место точек Р пересечения прямых MN и A'B' и есть квадратриса. уравнение в прямоугольных координатах: 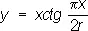; в полярных координатах: 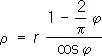. Часть квадратрисы, заключённая в квадрате OABC, была известна древнегреч. математикам. Открытие квадратрисы приписывается Гиппию Элидскому (5 в. до н. э.), использовавшему её для решения задачи о трисекции угла. Динострат (4 в. до н. э.) с помощью квадратрнсы выполнил квадратуру круга.

Трактриса (см. рис. «Трансцендентные кривые», № 2 ), кривая, для которой длина отрезка касательной от точки касания М до точки Р пересечения с данной прямой есть величина постоянная, равная а . Уравнение в прямоугольных координатах:

.

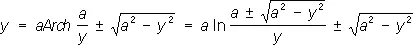Цепная линия (см. рис. «Трансцендентные кривые», № 3 ), кривая, форму которой принимает гибкая однородная и нерастяжимая тяжёлая нить, концы которой закреплены в двух точках. уравнение в прямоугольных координатах: у = a 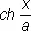= а ( e x/a+ е -х/a ) / 2.