БСЭ БСЭ - Большая Советская Энциклопедия (ЛИ)

y 0= C 1y 1 ( x ) + С 2у 2 ( х ) + ... + C ny n ( x ) ,

где C 1, C 2,..., C n — произвольные постоянные и y 1 ( x ) , у 2 ( х ) ,..., y n ( x ) — линейно независимые (см. Линейная зависимость ) частные решения, образующие т. н. фундаментальную систему решений. Критерием линейной независимости решений служит неравенство нулю (хотя бы в одной точке) определителя Вроньского ( вронскиана ) :

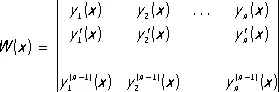(2)

Общее решение у = у ( х ) неоднородного Л. д. у. (1) имеет вид:

y = y 0+Y ,

где y 0= y 0 ( x ) — общее решение соответствующего однородного Л. д. у. и Y = Y ( x ) — частное решение данного неоднородного Л. д. у. Функция Y ( x ) может быть найдена по формуле:

,

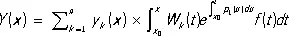где y k ( x ) — решения, составляющие фундаментальную систему решений однородного Л. д. у., и W k ( x ) — алгебраическое дополнение элемента y k ( n-1 )( x ) в определителе (2) Вроньского W ( x ).

Если коэффициенты уравнения (1) постоянны: p k ( x ) = a k ( k = 1, 2, ..., n ), то общее решение однородного уравнения выражается формулой:

,

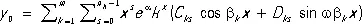где a k± ib k( k = 1, 2, ..., m ; 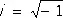) — корни т. н. характеристического уравнения:

l n+ a 1l n-1+ ... +a n= 0,

n k — кратности этих корней и C ks, D ks — произвольные постоянные.

Пример. Для Л. д. у. y’’’ + у = 0 характеристическое уравнение имеет вид: l 3+ 1 = 0. Его корнями являются числа:

l 1= -1; l 2= 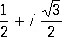и l 3=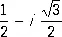

Следовательно, общее решение этого уравнения таково:

.

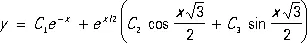Системы Л. д. у. имеют вид:

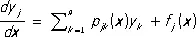(3)

( j = 1, 2, ..., n ).

Общее решение однородной системы Л. д. у. [получаемой из системы (3), если все f j ( x ) º 0] даётся формулами:

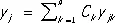
( j = 1, 2, ..., n )

где y j1, y j2, ..., y jn — линейно независимые частные решения однородной системы (т. е. такие, что определитель ½ y jk ( x )½ ¹ 0 хотя бы в одной точке).

В случае постоянных коэффициентов p jk ( x ) = a jk частные решения однородной системы следует искать в виде:

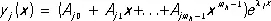
( j = 1, 2, ..., n ),

где A js — неопределённые коэффициенты, a l k— корни характеристического уравнения

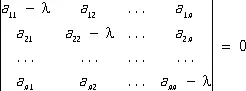
и m k — кратность этих корней. Полный анализ всех возможных здесь случаев проводится с помощью теории элементарных делителей [см. Нормальная (жорданова) форма матриц ] .

Для решения Л. д. у. и систем Л. д. у. с постоянными коэффициентами применяются также методы операционного исчисления.

Лит.: Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959; Смирнов В. И., Курс высшей математики, т. 2, 20 изд., М., 1967; т. 3, ч. 2, 8 изд., М., 1969; Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 3 изд., М., 1970.

Лине'йные систе'мы, колебательные системы, свойства которых не изменяются при изменении их состояния, т. е. параметры Л. с., характеризующие её свойства (упругость, масса и коэффициент трения механической системы; ёмкость, индуктивность и активное сопротивление электрической системы), не зависят от величин, характеризующих состояние системы (от смещений и скоростей в случае механической системы, напряжений и токов в случае электрической системы). Параметры реальных систем всегда в той или иной степени зависят от их состояния, например коэффициент упругости пружины зависит от величины деформации (отклонения от закона Гука при больших деформациях), активное сопротивление проводника зависит от его температуры, которая, в свою очередь, зависит от силы протекающего по проводнику тока и т. д. Поэтому реальные системы можно рассматривать как Л. с. только в некоторых ограниченных пределах изменений их состояния, при которых допустимо пренебречь изменениями их параметров. Для очень большого числа реальных систем эти пределы оказываются весьма широкими, поэтому большинство задач можно решать, рассматривая реальные системы как Л. с. Примерами Л. с. могут служить: маятник (при малых амплитудах колебания), электрический колебательный контур, мостовая измерительная схема, системы автоматического управления и регулирования и др. В тех случаях, когда в пределах возможных изменений состояний реальной системы уже сказываются изменения её параметров, приходится учитывать нелинейность системы (см. Нелинейные системы ) .

Л. с. обладают свойствами, существенно упрощающими анализ происходящих в них процессов. Процессы в Л. с. описываются линейными дифференциальными уравнениями (откуда и произошло их название). Причём, в различных по физической природе Л. с. процессы описываются одинаковыми по структуре уравнениями. На этом основано физ. и, в частности, электрическое моделирование Л. с., а также моделирование на ЦВМ. Л. с. играют большую роль в физике и технике, т. к. без искажения формы воспроизводят внешние воздействия, имеющие характер гармонических колебаний, и, во-вторых, в Л. с. справедлив суперпозиции принцип.

Лине'йные ускори'телизаряженных частиц, ускорители, в которых траектории частиц близки к прямой линии; см. Ускорители заряженных частиц.

Лине'йный дви'гатель, электродвигатель, у которого один из элементов магнитной системы разомкнут и имеет развёрнутую обмотку, создающую бегущее магнитное поле, а другой выполнен в виде направляющей, обеспечивающей линейное перемещение подвижной части двигателя. Л. д. постоянного тока состоит из якоря с расположенной на нём обмоткой, служащей одновременно коллектором (направляющий элемент), и разомкнутого магнитопровода с обмотками возбуждения (подвижная часть), расположенными так, что векторы сил, возникающих под полюсами магнитопровода, имеют одинаковое направление. Отличается простотой регулирования скорости перемещения подвижной части. Л. д. переменного тока могут быть асинхронными и синхронными. Якорь асинхронного Л. д. в виде бруска обычно прямоугольного сечения без обмоток закрепляется вдоль пути перемещения подвижной части двигателя, имеющей магнитопровод с развёрнутыми многофазными обмотками, питаемыми от источника переменного тока. Вследствие взаимодействия магнитного поля в магнитопроводе подвижной части с полем якоря возникают силы, которые заставляют перемещаться с ускорением подвижную часть Л. д. относительно неподвижного якоря до тех пор, пока скорости перемещения двигателя и бегущего магнитного поля не уравняются. Наиболее перспективно применение асинхронных Л. д. в тяговых электроприводах транспортных машин в сочетании с магнитными и воздушными подушками, что даёт возможность повысить скорость движения поездов до 450—500 км/ч. Синхронные Л. д. практически не изготовляются. Основное достоинство Л. д. — способность создавать большие усилия и, как следствие этого, возможность развития значительных ускорений, что особенно важно для транспортных средств, а также отсутствие редуктора в конструкции двигателя.