БСЭ БСЭ - Большая Советская Энциклопедия (МА)
- Название:Большая Советская Энциклопедия (МА)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (МА) краткое содержание
Большая Советская Энциклопедия (МА) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Данные первого столбца таблицы 1а собраны с целью установления точности изготовления деталей, расчётный диаметр которых равен 13,40 мм, при нормальном ходе производства. Простейшим допущением, которое может быть в этом случае обосновано некоторыми теоретическими соображениями, является предположение, что диаметры отдельных деталей можно рассматривать как случайные величины X , подчинённые нормальному распределению вероятностей
P{ X < x } = 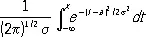 . (1)
. (1)
Если это допущение верно, то параметры a и s 2— среднее и дисперсию вероятностного распределения — можно с достаточной точностью оценить по соответствующим характеристикам статистического распределения (так как число наблюдений n = 200 достаточно велико). В качестве оценки для теоретической дисперсии s 2предпочитают не статистическую дисперсию D 2= S 2 / n , а несмещенную оценку
s 2= S 2/ ( n - 1).
Для теоретического среднего квадратичного отклонения не существует общего (пригодного при любом распределении вероятностей) выражения несмещенной оценки. В качестве оценки (вообще говоря, смещенной) для s чаще всего употребляют s . Точность оценок 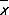 и s для a и s указывается соответствующими дисперсиями, которые в случае нормального распределения (1) имеют вид
и s для a и s указывается соответствующими дисперсиями, которые в случае нормального распределения (1) имеют вид
s 2 a= s 2 / n ~ s 2/ n ,
 ~ 2 s 4 / n ,
~ 2 s 4 / n ,
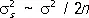 ~ s 2/ 2 n ,
~ s 2/ 2 n ,
где знак ~ обозначает приближённое равенство при больших n . Таким образом, уславливаясь прибавлять к оценкам со знаком ± их среднее квадратичное отклонение, имеем при больших n в предположении нормального распределения (1):
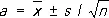 ,
, 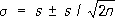 . (2)
. (2)
Для данных первого столбца таблицы 1а формулы (2) дают
a = 13,416 ± 0,008,
s = 0,110 ± 0,006.
Объём выборки n = 200 достаточен для законности пользования этими формулами теории больших выборок.
Дальнейшие сведения об оценке параметров теоретических распределений вероятностей см. в статьях Статистические оценки , Доверительные границы . О способах, при помощи которых по данным первого столбца таблицы 1а можно было бы проверить исходные гипотезы нормальности распределения и независимости наблюдений, см. в статьях Распределения , Непараметрические методы , Статистическая проверка гипотез .
При рассмотрении данных следующих столбцов таблицы 1а, каждый из которых составлен на основе 10 измерений, употребление формул теории больших выборок, установленных лишь в качестве предельных формул при n ® ¥, может служить только для первой ориентировки. В качестве приближённых оценок параметров a и s по-прежнему употребляются величины 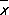 и s , но для оценки точности и надёжности таких оценок необходимо применять теорию малых выборок . При сравнении по правилам М. с. выписанных в последних строках таблицы 1а значений
и s , но для оценки точности и надёжности таких оценок необходимо применять теорию малых выборок . При сравнении по правилам М. с. выписанных в последних строках таблицы 1а значений 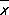 и s для трёх выборок с нормальными значениями a и s, оцененными по первому столбцу таблицы, можно сделать следующие выводы: первая выборка не даёт оснований предполагать существенного изменения хода производственного процесса, вторая выборка даёт основание к заключению об уменьшении среднего диаметра а , третья выборка — к заключению об увеличении дисперсии.
и s для трёх выборок с нормальными значениями a и s, оцененными по первому столбцу таблицы, можно сделать следующие выводы: первая выборка не даёт оснований предполагать существенного изменения хода производственного процесса, вторая выборка даёт основание к заключению об уменьшении среднего диаметра а , третья выборка — к заключению об увеличении дисперсии.
Все основанные на теории вероятностей правила статистической оценки параметров и проверки гипотез действуют лишь с определённым значимости уровнем w < 1, то есть могут приводить к ошибочным результатам с вероятностью a = 1 — w. Например, если в предположении нормального распределения и известной теоретической дисперсии s 2производить оценку a по 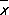 по правилу
по правилу
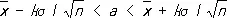 ,
,
то вероятность ошибки будет равна a, связанному с k соотношением (см. таблицу 3);
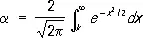 .
.
Вопрос о рациональном выборе уровня значимости в данных конкретных условиях (например, при разработке правил статистического контроля массовой продукции) является весьма существенным. При этом желанию применять правила лишь с высоким (близким к единице) уровнем значимости противостоит то обстоятельство, что при ограниченном числе наблюдений такие правила позволяют сделать лишь очень бедные выводы (не дают возможности установить неравенство вероятностей даже при заметном неравенстве частот и т. д.).
Таблица 3. — Зависимость a и w = 1 — a от k .
| k | 1,96 | 2,58 | 3,00 | 3,29 |
| a | 0,050 | 0,010 | 0,003 | 0,001 |
| w | 0,950 | 0,990 | 0,997 | 0,999 |
Выборочный метод.В предыдущем разделе результаты наблюдений, используемых для оценки распределения вероятностей или его параметров, подразумевались (хотя это и не оговаривалось) независимыми (см. Вероятностей теория и особенно Независимость ). Хорошо изученным примером использования зависимых наблюдений может служить оценка статистического распределения или его параметров в «генеральной совокупности» из N объектов по произведённой из неё «выборке», содержащей n < N объектов.
Терминологическое замечание. Часто совокупность n наблюдений, сделанных для оценки распределения вероятностей, также называют выборкой. Этим объясняется, например, происхождение употребленного выше термина «теория малых выборок». Эта терминология связана с тем, что часто распределение вероятностей представляют себе в виде статистического распределения в воображаемой бесконечной «генеральной совокупности» и условно считают, что наблюдаемые n объектов «выбираются» из этой совокупности. Эти представления не имеют отчётливого содержания. В собственном смысле слова выборочный метод всегда предполагает исходную конечную генеральную совокупность.
Примером применения выборочного метода может служить следующий. Пусть в партии из N изделий имеется L дефектных. Из партии отбирается случайным образом n < N изделий (например, n = 100 при N = 10 000). Вероятность того, что число l дефектных изделий в выборке будет равно m , равна
Читать дальшеИнтервал:
Закладка:
