БСЭ БСЭ - Большая Советская Энциклопедия (МА)

Если u 1= u 2, то пара ( i 0, j 0 ) составляет седловую точку игры, то есть выполняется двойное неравенство

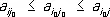; i = 1, …, m ; j = 1, …, n .

Число 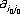называется значением игры; стратегии i 0 , j 0 называются оптимальным и чистыми стратегиями игроков I и II соответственно. Если u 1¹ u 2, то всегда u 1< u 2; в этом случае в игре седловой точки нет, а оптимальные стратегии игроков следует искать среди их смешанных стратегий (то есть вероятностных распределений на множестве чистых стратегий). В этом случае игроки оперируют уже с математическими ожиданиями выигрышей.

Основная теорема теории М. и. (теорема Неймана о минимаксе) утверждает, что в любой М. и. существуют оптимальные смешанные стратегии х* , у* , на которых достигаемые «минимаксы» равны (общее их значение есть значение игры). Например, игра с матрицей 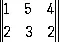имеет седловую точку при i 0 = 2, j 0 = 1, а значение игры равно 2; игра с матрицей 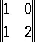не имеет седловой точки. Для неё оптимальные смешанные стратегии суть х* = ( 3/ 4, 1/ 4), y* = ( 1/ 2, 1/ 2); значение игры равно 1/ 2.

Для фактического нахождения оптимальных смешанных стратегий чаще всего используют возможность сведения М. и. к задачам линейного программирования . Можно использовать так называемый итеративный метод Брауна — Робинсон, состоящий в последовательном фиктивном «разыгрывании» данной игры с выбором игроками в каждой данной партии своих чистых стратегий, наилучших против накопленных к этому моменту стратегий оппонента. Игры, в которых один из игроков имеет только две стратегии, просто решить графически.

М. и. могут служить математическими моделями многих простейших конфликтных ситуаций из области экономики, математической статистики, военного дела, биологии. Нередко в качестве одного из игроков рассматривают «природу», под которой понимается вся совокупность внешних обстоятельств, неизвестных принимающему решения лицу (другому игроку).

Лит.: Матричные игры. [Сборник переводов], под редакцией Н. Н. Воробьева, М., 1961; Нейман Дж. фон, Моргенштерн О., Теория игр и экономическое поведение, перевод с английского, М., 1970; Оуэн Г., Теория игр, перевод с английского, М., 1971.

А. А. Корбут.

Матричные моделив экономике, один из наиболее распространённых типов экономико-математических моделей. Представляют собой прямоугольные таблицы ( матрицы ) , элементы которых отражают взаимосвязи экономических объектов и обладают определённым экономическим смыслом, значение которого вычисляется по установленным в теории матриц правилам. В М. м. отражается структура затрат на производство и распределение продукции и вновь созданной стоимости.

М. м. — балансово-нормативные, они объединяют в единой табличной форме балансы распределения продукции (по отдельным её видам) и увязанные с ними балансы затрат на её производство, а также нормативы материальных и денежных затрат. М. м. используются для экономического анализа и плановых расчётов с применением электронной вычислительной техники.

Представленная в графическом виде (см. схему) М. м. экономического объекта имеет вид прямоугольной таблицы, разделённой на 4 четверти (квадранта). Уравнения строк матрицы 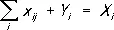, где элементы строки x ij — поставка продукции подразделения (отрасли) i в подразделение (отрасль) j , Y i — конечная продукция подразделения (отрасли) i , X i — валовая продукция подразделения (отрасли) i , представляют собой балансы распределения продукции, произведённой в различных производственных подразделениях (например, в цехах предприятия), в различных экономических объектах (предприятиях, объединениях), в разных отраслях народного хозяйства. Они имеют совершенно очевидный экономический смысл: сумма внутрипроизводственных поставок и конечного продукта составляет валовой выпуск подразделения (отрасли). Столь же очевиден смысл уравнения, составленного из элементов столбцов матрицы: 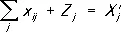, где x ij — затраты продукции подразделения (отрасли) j на производство продукции подразделения (отрасли) i , Z j — затраты первичных ресурсов и вновь созданная стоимость в подразделении (отрасли); X’ j — валовые затраты в сумме со вновь созданной стоимостью в подразделении (отрасли) j ,

X i = X’ j , если i тождественно j ; тогда в этом равенстве итогов одноимённых строк и столбцов находит выражение закон стоимости: стоимость распределённых и накопленных благ и услуг равна стоимости производственных затрат плюс вновь созданная стоимость. Из этого основного равенства М. м. вытекает целый ряд других производных уравнений, которые делают М. м. удобным расчётным плановым и аналитическим инструментом.

Таким образом, каждый показатель имеет двоякое значение: с одной стороны, он выражает объём поставок одного производственного подразделения (отрасли) в другое, с другой стороны — объём производственного потребления вторым подразделением продукции первого. I квадрант М. м. отражает, следовательно, внутрипроизводственные связи моделируемой экономической системы. Наиболее явное количественное выражение производственная структура получает в коэффициентах прямых затрат , которые представляют собой частное от деления объёмов затрат продукции всех подразделений на объём выпуска определённого подразделения: 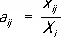. Тогда I квадрант М. м. приобретает смысл таблицы нормативов затрат, рассчитанных на единицу валового выпуска каждого вида продукции. В результате обращения инверсированной квадратной матрицы I квадранта получают коэффициенты полных затрат , выражающие совокупность прямых и косвенных затрат в расчёте на единицу конечного выпуска В = ( E — А ) -1. Во II квадранте отражаются результаты производственной и хозяйственной деятельности (конечная продукция); он рассматривается как выход модели. В III квадранте отражаются затраты первичных ресурсов, поступающих в систему извне, и вновь созданная стоимость (овеществленный труд); он рассматривается в качестве входа модели. В IV квадранте, где пересекаются строки III квадранта с колонками IV квадранта, отражаются, таким образом, транзитные процессы передачи материальных ресурсов и перераспределения стоимости: ресурсы, поступившие на вход данной экономической системы, используются в качестве конечных продуктов на выходе, минуя производственные подразделения.