БСЭ БСЭ - Большая Советская Энциклопедия (МА)

Действия над матрицами.Произведением прямоугольной ( m ´ n )-матрицы А на число ее называют М., элементы которой получены из элементов a ijумножением на число a:

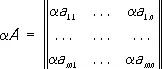
Сумма определяется для прямоугольных М. одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, то есть

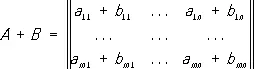
Умножение М. определяется только для прямоугольных М. таких, что число столбцов первого множителя равно числу строк второго. Произведением ( m ´ р )-матрицы А на ( р ´ n )-матрицу В будет ( m ´ n )-матрица С с элементами

c ij = a i1b 1j + a i2b 2j + ... + a ipb pj,

i = 1, ..., m , j = 1, ..., n .

Введённые три действия над М. обладают свойствами, близкими к свойствам действий над числами. Исключением является отсутствие коммутативного закона при умножении М.: равенство AB = BA может не выполняться. Матрицы А и В называются перестановочными, если AB = BA . Кроме того, произведение двух М. может равняться нулевой М., хотя каждый сомножитель отличен от нулевой. Справедливы правила:

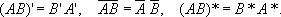
Определитель произведения двух квадратных М. равен произведению определителей перемножаемых М.

Часто удобно разбивать М. на клетки, являющиеся М. меньших размеров, проводя разделительные линии через всю М. слева направо или сверху вниз. При умножении такой так называемой клеточной М. на число, нужно умножить все её клетки на то же число. При надлежащем согласовании разбиений действия сложения и умножения клеточных М. осуществляются так, как будто вместо клеток стоят числа.

Квадратная М. А = ( a ij ) называется неособенной, или невырожденной, если её определитель не равен нулю; в противном случае М. называется особенной (вырожденной). М. А -1называется обратной к квадратной М. А , если AA - 1= E , при этом 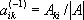. Неособенность М. А есть необходимое и достаточное условие существования обратной М., которая при этом оказывается единственной и перестановочной с исходной М. Верна формула: ( AB ) -1= B -1 A -1.

Большой интерес приобретает обобщённая обратная (или псевдообратная) М. А +, определяемая как для любой прямоугольной М., так и для особенной квадратной. Эта М. определяется из четырёх равенств:

AA + A = A , А + АА += А , AA += ( AA +)*, А + А = ( А + А )*.

Квадратные матрицы.Степенью A n М. А называется произведение n сомножителей, равных А . Выражение вида a 0 А n + a 1 A n-1 + ... + a n E , где a 0, a 1, ..., a n— числа, называется значением полинома a 0 t n + a i t n-1 + ... + a n E от квадратной М. А . Правила действий над полиномами от данной М. А ничем не отличаются от правил действий над алгебраическими многочленами. Можно рассматривать и аналитические функции от М. В частности, если

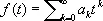
есть сходящийся на всей комплексной плоскости ряд (например, 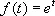), то и бесконечный ряд 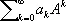оказывается сходящимся при любой М. А , его сумму естественно считать равной f(A) . Если же ряд f(t) сходится в некотором конечном круге сходимости, то f(A) задаётся этим рядом для достаточно «малых» М.

Аналитические функции от М. играют большую роль в теории дифференциальных уравнений. Так, система обыкновенных дифференциальных уравнений с постоянными коэффициентами, записанных в матричных обозначениях в виде

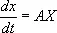
(здесь Х — столбец из неизвестных функций), имеет решение х = e AtC , где С — столбец из произвольных постоянных.

Ненулевой столбец Х такой, что AX = l Х , называется собственным вектором М. А . В этом равенстве коэффициент l может быть лишь одним из корней многочлена

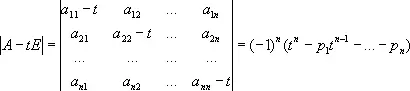
который называется характеристическим многочленом М. А . Эти корни называются собственными значениями, или характеристическими числами, М. А . Коэффициенты характеристического многочлена выражаются через суммы некоторых миноров М. А. В частности, p 1 = a 11 + ... + a 1n = Sp A (след A ), 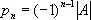. Справедливо соотношение Кэли — Гамильтона: если j( f ) есть характеристический многочлен М. А , то j( A ) = 0, так что М. А является «корнем» своего характеристического многочлена.

М. А называется подобной М. В, если существует такая неособенная М. С , что В = С -1AС . Легко проверяется, что подобные М. имеют одинаковые характеристические многочлены.

Исчисление матриц. М. — полезный аппарат для исследования многих задач теоретической и прикладной математики. Одной из важнейших задач является задача нахождения решения систем линейных алгебраических уравнений. В матричных обозначениях такие системы записываются в виде

AX = F ,

где A есть М. коэффициентов, Х — искомое решение, записанное в виде столбца из n элементов, F — столбец свободных членов из m элементов. Если А — квадратная неособенная М., то система имеет единственное решение Х = A -1F . Если A прямоугольная ( m ´ n -матрица ранга k , то решение может не существовать или быть не единственным. В случае несуществования решения имеет смысл обобщённое решение, дающее минимум сумме квадратов невязок (см. Наименьших квадратов метод ). При отсутствии единственности точного или обобщённого решения часто выбирают нормальное решение, то есть решение с наименьшей суммой квадратов компонент. Нормальное обобщённое решение находится по формуле Х = A + F . Наиболее важен случай переопределённой системы: k = n < m . В этом случае обобщённое решение единственно. При k = m < n (недоопределённая система) точных решений бесконечно много и формула даёт нормальное решение.