БСЭ БСЭ - Большая Советская Энциклопедия (МА)
- Название:Большая Советская Энциклопедия (МА)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (МА) краткое содержание
Большая Советская Энциклопедия (МА) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
В строкоотливной наборной машине (см. Линотип ) из отдельных М., хранящихся в магазине, составляется матричная строка, устанавливаемая перед щелью литейной формы. После заполнения формы сплавом образуется цельнометаллическая шрифтовая строка.
В буквоотливной наборной машине (см. Монотип ) комплект М. собран в матричной рамке. При отливке необходимая М. устанавливается над щелью отливной формы. В отличие от строкоотливной шрифтовая строка на буквоотливной наборной машине образуется из отдельных литер. Монотипная М. снабжена отверстием для нанизывания на стержень матричной рамки и коническим углублением для точной установки и прижима М. к литейной форме.
В фотонаборных машинах используются М., в которых углублённые изображения знаков заменены фотографическими.
2) Углублённый оттиск с рельефной печатной формы на пластичном материале (картоне, пластмассе и т. д.), используемый для получения стереотипных копий печатной формы (см. Матрицирование , Стереотипия ).
Г. С. Ершов.
Матрица рассеяния
Ма'трица рассе'яния, S -maтрица, совокупность величин ( матрица ), описывающая процесс перехода квантовомеханических систем из одних состояний в другие при их взаимодействии (рассеянии). Понятие «М. р.» введено В. Гейзенбергом в 1943.
При рассеянии система переходит из одного квантового состояния, начального (его можно отнести к моменту времени t = —¥) в другое, конечное ( t = +¥). Если обозначить набор квантовых чисел , характеризующих начальное состояние, через i , а конечное — через f , то амплитуда рассеяния (квадрат модуля которой определяет вероятность данного рассеяния) может быть записана как S fi . Совокупность амплитуд рассеяния образует таблицу с двумя входами ( i — номер строки, f — номер столбца), которая и называется М. р. S . Каждая амплитуда является элементом этой матрицы (матричным элементом). Наборы квантовых чисел i , f могут содержать как непрерывные величины (энергию, угол рассеяния и другие), так и дискретные (орбитальное квантовое число, спин , изотопический спин , массу и т. д.). В простейшем случае системы двух бесспиновых частиц в нерелятивистской квантовой механике состояние определяется относительным импульсом частиц р ; тогда амплитуда рассеяния представляет собой функцию двух переменных — энергии Е и угла рассеяния J
S fi = F ( E , J).
В общем случае М. р. содержит элементы, отвечающие как упругому рассеянию, так и процессам превращения и рождения частиц. Квадрат модуля матричного элемента ½ S fi ½ 2определяет вероятность соответствующего процесса (или его эффективное поперечное сечение).
Нахождение М. р. — основная задача квантовой механики и квантовой теории поля. М. р. содержит всю информацию о поведении системы, если известны не только численные значения, но и аналитические свойства (см. Аналитические функции ) её элементов; в частности, её полюсы (см. Особая точка ) определяют связанные состояния системы (а следовательно, дискретные уровни энергии). Из основных принципов квантовой теории следует важнейшее свойство М. р. — её унитарность. Оно выражается в виде соотношения SS + = 1 [ S + — матрица, эрмитово сопряжённая S , то есть ( S + ) fi = S* if , где знак* означает комплексное сопряжение] или
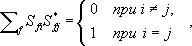
и отражает тот факт, что сумма вероятностей рассеяния по всем возможным каналам реакции должна равняться единице. Соотношение унитарности позволяет устанавливать важные соотношения между различными процессами, а в некоторых случаях даже полностью решить задачу. В релятивистской квантовой механике существует направление, в котором М. р. считается первичной динамической величиной; требования унитарности и аналитичности М. р. должны служить при этом основой построения полной системы уравнений, определяющей матрицу S .
В. Б. Берестецкий.
Матрицирование
Матрици'рование, полиграфическая операция для воспроизведения углублённого изображения графических элементов (штриховых и полутоновых) с оригинальной печатной формы в листах матричного материала способом прессования для последующего изготовления стереотипов. В состав оригинальной рельефной формы входят текстовой набор, изготовленный на строко- и буквоотливных машинах или набранный вручную, цинкографские клише и пробельные элементы, вмонтированные в общую заключную раму. В качестве матричного материала для литых металлических стереотипов используют термостойкий картон толщиной 0,5—1 мм , для гальваностереотипов — листы винипласта или калиброванного по толщине свинца (1—2 мм ), а для пластмассовых и резиновых стереотипов — фильтровальный картон, пропитанный бакелитовым лаком и покрытый специальным слоем. При М. листы матричного материала, уложенные на оригинальную форму, покрывают сверху эластичной прокладкой из кирзы, резино-тканевого материала, или поропласта. М. производят чаще всего в прессах гидравлического действия с различной степенью механизации и автоматизации. Рабочий пакет, состоящий из оригинальной формы, матричного материала и эластичного настила, укладывают на нижнюю плиту пресса и подъёмом этой плиты или опусканием верхней создают необходимое для прессования давление. Давление в зависимости от состава оригинальной печатной формы и характера матричного материала создаётся в широких пределах от 1 до 20 Мн/м 2 (от 10 до 200 кгс/см 2 ), а для свинцовых матриц до 120 Мн/м 2 .
П. Я. Розенфельд.
Матричные игры
Ма'тричные и'гры, понятие игр теории . М. и. — игры, в которых участвуют два игрока (I и II) с противоположными интересами, причём каждый игрок имеет конечное число чистых стратегий . Если игрок I имеет m стратегий, а игрок II — n стратегий, то игра может быть задана ( m ´ n )-maтрицей А = || a ij||, где a ijесть выигрыш игрока I, если он выберет стратегию i ( i = -1, ..., m ), а игрок II — стратегию j ( j = 1, ..., n ). Следуя общим принципам поведения в антагонистических играх (частным случаем которых являются М. и.), игрок I стремится выбрать такую стратегию i 0 , на которой достигается
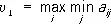 ;
;
игрок II стремится выбрать стратегию j o , на которой достигается
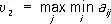 ;
;
Интервал:
Закладка:
