БСЭ БСЭ - Большая Советская Энциклопедия (МН)

Простейшими М. п. являются n -мерные евклидовы пространства, где n может быть любым натуральным числом. Подобно тому, как положение точки обычного евклидова пространства определяется заданием трёх её прямоугольных координат, «точка» n -мерного евклидова пространства задаётся n «координатами» x 1 , x 2 , ..., x n (которые могут принимать любые действительные значения); расстояние r между двумя точками M ( x 1 , x 2 , ..., x n ) и М' ( у 1 , y 2 , ..., y n) определяется формулой

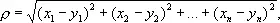
аналогичной формуле расстояния между двумя точками обычного евклидова пространства. С сохранением такой же аналогии обобщаются на случай n -мерного пространства и другие геометрические понятия. Так, в М. п. рассматриваются не только двумерные плоскости, но и k -мерные плоскости ( k < n ), которые, как и в обычном евклидовом пространстве, определяются линейными уравнениями (или системами таких уравнений).

Понятие n -мерного евклидова пространства имеет важные применения в теории функций многих переменных, позволяя трактовать функцию n переменных как функцию точки этого пространства и тем самым применять геометрические представления и методы к изучению функций любого числа переменных (а не только одного, двух или трёх). Это и было главным стимулом к оформлению понятия n -мерного евклидова пространства.

Важную роль играют и другие М. п. Так, при изложении физического принципа относительности пользуются четырёхмерным пространством, элементами которого являются т. н. «мировые точки». При этом в понятии «мировой точки» (в отличие от точки обычного пространства) объединяется определённое положение в пространстве с определённым положением во времени (поэтому «мировые точки» и задаются четырьмя координатами вместо трёх). Квадратом «расстояния» между «мировыми точками» М’ ( х’, y’, z’, t’ ) и М’’ ( х’’, y’’, z’’, t’’ ) (где первые три «координаты» — пространственные, а четвёртая — временная) естественно считать здесь выражение

( M’ M’’ ) 2= ( x’ - x’’ ) 2+ ( y’ — y’’ ) 2+ ( z’ — z’’ ) 2— c 2 ( t’ — t’’ ) 2,

где с — скорость света. Отрицательность последнего члена делает это пространство «псевдоевклидовым».

Вообще n -мерным пространством называется топологическое пространство, которое в каждой своей точке имеет размерность n . В наиболее важных случаях это означает, что каждая точка обладает окрестностью, гомеоморфной открытому шару n -мерного евклидова пространства.

Подробнее о развитии понятия М. п., геометрии М. п., а также лит. см. в ст. Геометрия.

Многому'жество,см. Полиандрия.

Многоно'жки(Myriapoda), общее название 4 классов наземных членистоногих животных: губоногих, двупарноногих, симфил и пауропод; прежде считались одним классом. Тело М. состоит из головы и более или менее длинного сегментированного туловища. Усиков 1 пара; ноги имеются на всех (или почти на всех) туловищных сегментах. Около 11 тыс. видов; в СССР около 1000 видов. Обитают в почве, лесной подстилке, гнилой древесине. Питаются гниющими растительными остатками (двупарноногие, симфилы), мицелием грибов (пауроподы); некоторые — хищники (губоногие).

Многоно'жковые(Polypodiaceae), семейство растений из класса папоротников. Многолетники с ползучими или иногда восходящими корневищами, покрытыми чешуйками. Листья перистые, дважды перистые, лопастные или цельные. Около 65 родов (до 1200 видов), растут преимущественно в тропиках, где они часто развиваются как эпифиты. В СССР 5 видов М.: 1 дальневосточный из рода пиррозия (Pyrrosia) и 4 из рода многоножка (Polypodium). Многоножка обыкновенная, или сладкий папоротник (P. vulgare), растет в Европейской части СССР, на Кавказе, в Средней Азии и Западной Сибири; имеет сладковатое корневище. Многие тропические М. (Drynaria, Platycerium и др.) разводят в оранжереях и комнатах.

Лит.: Тахтаджян А. Л., Высшие растения, т. 1, М. — Л., 1956.

Многоножка обыкновенная.

Многообра'зие,математическое понятие, уточняющее и обобщающее на любое число измерений понятия линии и поверхности, не содержащих особых точек (т. e. линии без точек самопересечения, концевых точек и т. п. и поверхности без самопересечений, краев и т. п.).

Примером одномерного М. могут служить прямая, парабола, окружность, эллипс, вообще любая линия, у каждой точки которой существует окрестность, являющаяся взаимно однозначным и непрерывным (или, как говорят в топологии, гомеоморфным) образом интервала (внутренней части отрезка прямой). Интервал сам является одномерным М., отрезок же не является М. (так как концы его не имеют окрестностей указанного вида).

Примером двумерного М. может служить любая область на плоскости (например, внутренность круга x 2+ y 2< r 2), сама плоскость, параболоид, сфера, эллипсоид, тор и т. п. Двумерные М. характеризуются тем, что у каждой их точки имеется окрестность, гомеоморфная внутренности круга. Это требование исключает, например, из числа двумерных М. коническую поверхность (её вершина, в которой сходятся две её полости, не имеет требуемого вида окрестности). Однако выделяют специальный класс объектов, которые не удовлетворяют этому требованию, — т. н. многообразия с краем (например, замкнутый круг x 2+ y 2£ r 2).

Примером трёхмерного М. может служить обычное евклидово пространство, а также любое открытое множество в евклидовом пространстве. Трёхмерные М. характеризуются тем, что у каждой их точки имеется окрестность, гомеоморфная внутренности шара.

М. разделяются на замкнутые и открытые (определение см. ниже). В случае одного измерения каждое замкнутое М. гомеоморфно окружности, а каждое открытое — прямой (на рис. 1 изображены одномерные М. и окрестности точки Р на каждом из них). В случае двух измерений уже замкнутые М. довольно разнообразны. Они распадаются на бесконечное число топологических типов: сфера — поверхность рода 0 ( рис. 2 , а), тор — поверхность рода 1 ( рис. 2 , б), «крендель» — поверхность рода 2 ( рис. 2 , в), вообще «сфера с n ручками» — поверхность рода n (на рис. 2 , г изображена такая поверхность при n = 3). Этими примерами исчерпываются все топологические типы замкнутых двумерных ориентируемых М. (см. также Ориентируемая поверхность ) . Существует ещё бесконечное число замкнутых двумерных неориентируемых М. — односторонних поверхностей, например проективная плоскость, т. н. односторонний тор ( Клейна поверхность ) . Имеется и классификация открытых двумерных М. Полная классификация М. трёх измерений не найдена (1974) (даже для случая замкнутых М.).