БСЭ БСЭ - Большая Советская Энциклопедия (МН)
- Название:Большая Советская Энциклопедия (МН)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (МН) краткое содержание
Большая Советская Энциклопедия (МН) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Многообразием n измерений (или n -мерным многообразием) называется всякое хаусдорфово топологическое пространство, обладающее следующим свойством: каждая его точка имеет окрестность, гомеоморфную внутренности n -мерного шара, и всё пространство может быть представлено в виде суммы конечного или бесконечного (счётного) множества таких окрестностей. М. называется замкнутым, если оно компактно (см. Компактность ) , в противном случае — открытым. Иногда к определению М. прибавляют ещё требование его связности: каждые две точки М. могут быть в нём соединены непрерывной дугой.
Введение в математику понятия М. любого (натурального) числа измерений n было вызвано весьма разнообразными потребностями геометрии, математического анализа, механики и физики. Важность достаточной широты понимания М. как топологического пространства основана на том, что точками так определённых М. могут быть объекты любой природы, например прямые, сферы, матрицы и т. д.
При надлежащем добавлении требований к определению М. устанавливается понятие гладкого, или дифференцируемого, многообразия. На гладком М. имеется возможность рассматривать дифференцируемые функции и дифференцируемые отображения в себя или в другие гладкие М. Гладкие М. имеют особенно большое значение в современной математике, поскольку именно они наиболее широко используются в приложениях и смежных областях (например, конфигурационные пространства и фазовые пространства в механике и физике). На гладких М. можно ввести метрику, превратив его в риманово пространство. Это позволяет строить дифференциальную геометрию на М. Например, введя некоторым образом метрику в конфигурационном пространстве механической системы, можно истолковать траектории движения как геодезические линии в этом пространстве (см. Наименьшего действия принцип ) . М., для элементов которого определено (дифференцируемое) умножение, превращающее М. в группу, называется группой Ли (см. Непрерывная группа ) .
Понятие М. играет большую роль в теории алгебраических функций, непрерывных групп и т. д. Во всех этих приложениях существенны свойства М., не изменяющиеся при топологических преобразованиях, — т. н. топологические свойства. К ним относятся, например, ориентируемость или неориентируемость М. (см. Ориентация ) . Изучение этих свойств является одной из важнейших задач топологии.
Лит.: Александров П. С. и Ефремович В. А., Очерк основных понятий топологии, М. — Л., 1936; Александров П. С., Комбинаторная топология, М. — Л., 1947; Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967.
Н. В. Ефимов.
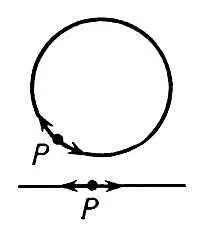
Рис. 1. Одномерные многообразия.
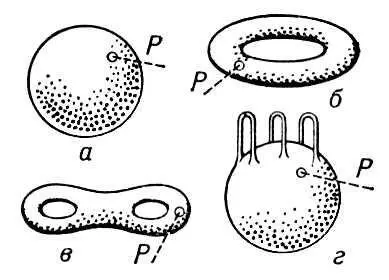
Рис. 2. Примеры замкнутых двумерных многообразий.
Многоосный автомобиль
Многоо'сный автомоби'ль,автомобиль, имеющий число осей более двух. Многоосными чаще всего выполняются грузовые автомобили и тягачи, реже автобусы и троллейбусы. М. а. благодаря распределению общего веса на большее число осей имеют, как правило, большую грузоподъёмность и повышенную проходимость по сравнению с двухосными. Недостатки М. а. — их повышенная стоимость и большие расходы на эксплуатацию.
Первая попытка создания М. а. относится к 1898; серийное производство началось в середине 1920-х гг. на заводе «Рено» (Франция). В СССР выпуск М. а. (ЯГ-10) грузоподъёмностью 8 т начал Ярославский автомобильный (ныне моторный) завод в 1932.
Краткая техническая характеристика многоосных автомобилей, выпускаемых в СССР
| Показатели | Mapка автомобиля | ||||||
| ЗИЛ-131 | Урал-375Д | КамАЗ | КрАЗ-257 | КрАЗ-255Б | МАЗ-516A | MA3-537A | |
| Колёсная формула | 6´6 | 6´6 | 6´4 | 6´4 | 6´6 | 6´2 | 8´8 |
| Грузоподъёмность, т | 3,5 | 4,5 | 8,0 | 12,0 | 7,5 | 14,5 | 15,0 |
| Снаряженный вес, т | 6,46 | 8,4 | — | 11,13 | 11,95 | 8,8 | 22,5 |
| Мощность двигателя, квт (л. с.) | 110(150) | 132(180) | 154(210) | 176(240) | 176(240) | 132(180) | 386(525) |
| Скорость, км/ч | 80 | 75 | 80 | 70 | 70 | 85 | 60 |
| Контрольный расход топлива, л/100 км | 40 | 48 | — | 36 | 40 | 30 | 125 |
В зависимости от числа колёс принято характеризовать автомобили т. н. колёсной формулой, где первая цифра указывает на общее число колёс, а вторая — на число ведущих колёс (считая сдвоенное колесо за одно). М. а. выполняются трёх- и четырёхосными, а в отдельных случаях и пятиосными. М. а. первой группы (четырёхосные, рис. , а — е) выпускаются в сравнительно небольших количествах и применяются в основном для геологоразведочных работ, в строительстве, в войсковых подразделениях. М. а. второй группы (трёхосные, рис. , ж — м) более распространены и применяются для магистральных перевозок грузов; к ним относятся междугородные и сочленённые городские автобусы.
Машины повышенной проходимости (грузовые, специальные автомобили, тягачи, бронетранспортёры) выполняются со всеми ведущими колёсами. Краткие технические характеристики М. а., выпускаемых в СССР, приведены в табл.
Развитие конструкций М. а. повышенной проходимости осуществляется за счёт создания сочленённых автомобилей с числом осей от 3 до 6; в дорожных М. а. намечается тенденция к более широкому использованию схем, показанных на рис. , д, к и л (для грузовых автомобилей) и рис. , к и м (для автобусов).
Лит.: Колесные автомобили высокой проходимости, М., 1967; Селиванов И. И., Автомобили и транспортные гусеничные машины высокой проходимости, М., 1967; Краткий автомобильный справочник, 6 изд., М., 1971.
Л. М. Шугуров.
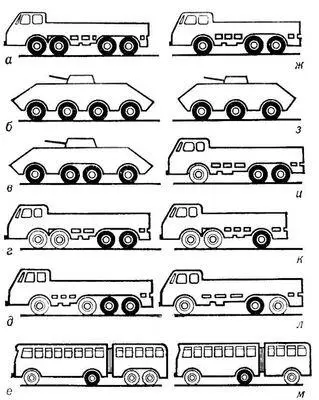
Схемы многоосных автомобилей (ведущие колёса выделены чёрным цветом): а — МАЗ-537А (СССР), Татра-813 (ЧССР); б — БТР-60П (СССР), ДАФ (Нидерланды); в — Панар-ЭБР (Франция); г — АЕК-Маммут (Великобритания); д — Скэммель-Самсон (Великобритания); е — СВАРЗ (СССР); ж — ЗИЛ-131 и Урал-375 (СССР); э — Альвис (Великобритания); и — КрАЗ-257 (СССР); к — Бюссинг-Суперкарго (ФРГ), ФИАТ-590НА (Италия); л — МАЗ-516 (СССР); м — Икарус-180 (ВНР), Шкода-ШМ 16,5 (ЧССР).
Многопёры
Многопёры(Polypterus), род рыб надотряда многопёрых. Тело вытянутое (длиной до 120 см ) , слабо сжатое с боков. Грудные плавники в основании имеют мясистую лопасть, спинной — из ряда плавничков, имеющих спереди по жёсткому лучу, брюшные — отнесены далеко назад. Тело покрыто ганоидной чешуей. Плавательный пузырь двойной, ячеистый, открывается с брюшной стороны и играет роль «лёгкого». М. поднимаются наверх и заглатывают воздух; лишённые возможности дышать атмосферным воздухом, М. гибнут через 2—3 ч, но и вне воды они жить не могут. 10 видов. Населяют тихие заводи рек и лагуны озёр Африки. Питаются мелкой рыбой и беспозвоночными. Нерест в июле — сентябре (в период дождей), икра мелкая (до 1—3 мм ) , сильно пигментирована. Из икры выходят личинки с наружными жабрами. Промысловое значение невелико; мясо вкусное. Некоторые виды содержат в аквариумах.
Читать дальшеИнтервал:
Закладка:
