БСЭ БСЭ - Большая Советская Энциклопедия (ОР)
- Название:Большая Советская Энциклопедия (ОР)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (ОР) краткое содержание
Большая Советская Энциклопедия (ОР) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Лит.: Толстов Г. П., Ряды Фурье, 2 изд., М., 1960; Натансон И. П., Конструктивная теория функций, М. — Л., 1949; его же, Теория функций вещественной переменной, 2 изд., М., 1957; Джексон Д., Ряды Фурье и ортогональные полиномы, пер. с англ., М., 1948; Качмаж С., Штейнгауз Г., Теория ортогональных рядов, пер. с нем., М., 1958.
Ортогональное преобразование
Ортогона'льное преобразова'ние, линейное преобразование евклидова векторного пространства, сохраняющее неизменным длины или (что эквивалентно этому) скалярное произведение векторов. В ортогональном и нормированном базисе О. п. соответствует ортогональная матрица . О. п. образуют группу — т.н. группу вращений данного евклидова пространства вокруг начала координат. В трёхмерном пространстве О. п. сводится к повороту на некоторый угол вокруг некоторой оси, проходящей через начало координат О , если определитель соответствующей ортогональной матрицы равен +1. Если же этот определитель равен —1, то поворот дополняется зеркальным отражением относительно плоскости, проходящей через О и перпендикулярной оси поворота. В двумерном пространстве, т. е. в плоскости, О. п. определяет поворот на некоторый угол вокруг начала координат О или зеркальное отражение относительно некоторой прямой, проходящей через О . Используется О. п. при приведении к главным осям квадратичной формы . См. также Матрица , Векторное пространство .
Ортогональность
Ортогона'льность(греч. orthogōnios — прямоугольный, от orthós — прямой и gōnía — угол), обобщение (часто синоним) понятия перпендикулярности . Если два вектора в трёхмерном пространстве перпендикулярны, то их скалярное произведение равно нулю. Это позволяет обобщить понятие перпендикулярности, распространив его на векторы в любом линейном пространстве, в котором определено скалярное произведение, обладающее обычными свойствами (см. Гильбертово пространство ), назвав два вектора ортогональными, если их скалярное произведение равно нулю. В частности, вводя скалярное произведение в пространстве комплекснозначных функций, заданных на отрезке [ а , b ] формулой
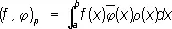 ,
,
где r( х ) ³ 0, называют две функции f ( x ) и j( x ), для которых ( f , j) r= 0, то есть
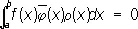 ,
,
ортогональными с весом r( х ). Два линейных подпространства называется ортогональными, если каждый вектор одного из них ортогонален каждому вектору другого. Это понятие обобщает понятие перпендикулярности двух прямых или прямой и плоскости в трёхмерном пространстве (но не понятие перпендикулярности двух плоскостей). Термином ортогональные кривые обозначают кривые линии, пересекающиеся под прямым углом (измеряется угол между касательными в точке пересечения). См., например, ортогональные траектории в ст. Изогональные траектории .
Ортогональные многочлены
Ортогона'льные многочле'ны,специальные системы многочленов { р п ( х )}; n = 0, 1, 2,..., ортогональных с весом r( х ) на отрезке [ а , b ] (см. Ортогональная система функций ). Нормированная система О. м. обозначается через 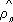 , а система О. м., старшие коэффициенты которых равны 1,— через
, а система О. м., старшие коэффициенты которых равны 1,— через 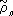 . В краевых задачах математической физики часто встречаются системы О. м., для которых вес r( х ) удовлетворяет дифференциальному уравнению (Пирсона)
. В краевых задачах математической физики часто встречаются системы О. м., для которых вес r( х ) удовлетворяет дифференциальному уравнению (Пирсона)
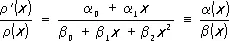
Многочлен р п ( х ) такой системы удовлетворяет дифференциальному уравнению
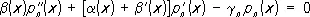
где g n = n [(a 1+ ( n + 1)b 2].
Наиболее важные системы О. м. (классические) относятся к этому типу; они получаются (с точностью до постоянного множителя) при указанных ниже а , b и r( х ).
1) Якоби многочлены { Р п ( l, m)( х )} — при а = —1, b = 1 r( х ) = (1— х ) l(1 + x ) m, l > —1, m > —1. Специальные частные случаи многочленов Якоби соответствуют следующим значениям l и m: l = m— ультрасферические многочлены 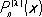 (их иногда называют многочленами Гегенбауэра); l = m = — 1/ 2, т. е.
(их иногда называют многочленами Гегенбауэра); l = m = — 1/ 2, т. е. 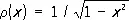 — Чебышева многочлены 1-го рода T n ( x ); l = m = 1/ 2, т. е.
— Чебышева многочлены 1-го рода T n ( x ); l = m = 1/ 2, т. е. 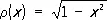 — Чебышева многочлены 2-го рода U n ( x ); l = m = 0, т. е. r( х ) º1 — Лежандра многочлены Р п ( х ).
— Чебышева многочлены 2-го рода U n ( x ); l = m = 0, т. е. r( х ) º1 — Лежандра многочлены Р п ( х ).
2) Лагерра многочлены L n ( x ) — при а = 0, b = + ¥ и r( х ) = е —х (их наз. также многочленами Чебышева — Лагерра) и обобщённые многочлены Лагерра 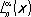 — при
— при 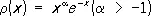 .
.
3) Эрмита многочлены Н n ( х ) — при а = —¥, b = + ¥ и 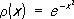 (их называют также многочленами Чебышева — Эрмита).
(их называют также многочленами Чебышева — Эрмита).
О. м. обладают многими общими свойствами. Нули многочленов р n ( х ) являются действительными и простыми и расположены внутри [ а , b ]. Между двумя последовательными нулями многочлена р n ( х ) лежит один нуль многочлена p n+1 ( х ). Многочлен р n ( х ) может быть представлен в виде т. н. формулы Родрига
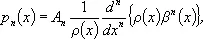
где A n — постоянное, а b( х ) см. формулу (*). Каждая система О. м. обладает свойствами замкнутости. Три последовательных О. м. 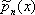 ,
, 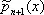 ,
, 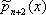 связаны рекуррентным соотношением:
связаны рекуррентным соотношением:
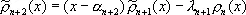 ,
,
Интервал:
Закладка:
