БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

После'довательный ана'лизв математической статистике, способ статистической проверки гипотез, при котором необходимое число наблюдений не фиксируется заранее, а определяется в процессе самой проверки. Во многих случаях для получения столь же обоснованных выводов применение надлежащим образом подобранного способа П. а. позволяет ограничиться значительно меньшим числом наблюдений (в среднем, т.к. число наблюдений при П. а. есть величина случайная), чем при способах, в которых число наблюдений фиксировано заранее.

Пусть, например, задача состоит в выборе между гипотезами H 1 и H 2 по результатам независимых наблюдений. Гипотеза H 1 заключается в том, что случайная величина Х имеет распределение вероятностей с плотностью f 1 (x), a H 2— в том, что Х имеет плотность f 2 ( x ) . Для решения этой задачи поступают следующим образом. Выбирают два числа А и В (0 < A < B ) . После первого наблюдения вычисляют отношение l 1= f 2 ( x 1 ) /f 1 ( x 1 ) , где x 1 — результат первого наблюдения. Если l 1< A, принимают гипотезу H 1; если l 1> B, принимают H 2, если A £ l 1£ B , производят второе наблюдение и так же исследуют величину l 2= f 2 ( x 1 ) f 2 ( x 2 ) /f 1 ( x 1 ) f 1 ( x 2 ) , где x 2— результат второго наблюдения, и т.д. С вероятностью, равной единице, процесс оканчивается либо выбором H 1, либо выбором H 2. Величины А и В определяются из условия, чтобы вероятности ошибок первого и второго рода (т. е. вероятность отвергнуть гипотезу H 1 , когда она верна, и вероятность принять H 1, когда верна H 2 ) имели заданные значения a 1и a 2. Для практических целей вместо величины l n удобнее рассматривать их логарифмы. Пусть, например, гипотеза H 1 состоит в том, что Х имеет нормальное распределение

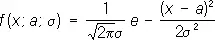
с a = 0 , s = 1, гипотеза H 2— в том, что X имеет нормальное распределение с a = 0,6, s = 1, и пусть a 1= 0,01, a 2= 0,03. Соответствующие подсчёты показывают, что в этом случае

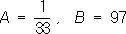
и logl n= 0.6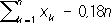

Поэтому неравенства 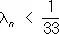и 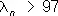равносильны неравенствам

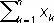< 0.3 n - 5.83

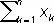> 0.3 n + 7.62

соответственно. Процесс П. а. допускает при этом простое графическое изображение (см. рис. ). На плоскости ( хОу ) наносятся две прямые y = 0.3 x - 5.83 и y = 0.3 x + 7.62 и ломаная линия с вершинами в точках ( n , 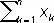) , n = 1 , 2,.... Если ломаная впервые выходит из полосы, ограниченной этими прямыми, через верхнюю границу, то принимается H 2, если через нижнюю, — H 1. В приведённом примере для различения H 1 и H 2 методом П. а. требуется в среднем не более 25 наблюдений. В то же время для указанного различения гипотез H 1 и H 2 по выборкам фиксированного объёма потребовалось бы более 49 наблюдений.

Лит.: Блекуэлл Д., Гиршик М. А., Теория игр и статистических решений, пер. с англ., М., 1958: Вальд А., Последовательный анализ, пер. с англ., М., 1960; Ширяев А. Н., Статистический последовательный анализ, М., 1969.

Ю. В. Прохоров.

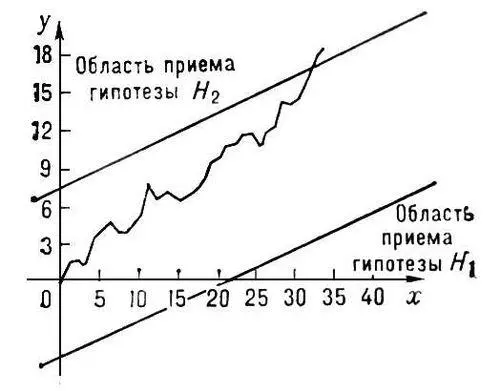
Графическое изображение процесса последовательного анализа.

После'довательных приближе'нии ме'тод,метод решения математических задач при помощи такой последовательности приближении, которая сходится к решению и строится рекуррентно (т. е. каждое новое приближение вычисляют, исходя из предыдущего; начальное приближение выбирается в достаточной степени произвольно). П. п. м. применяется для приближённого нахождения корней алгебраических и трансцендентных уравнений, для доказательства существования решения и приближённого нахождения решений дифференциальных, интегральных и интегро-дифференциальных уравнений, для качественной характеристики решения и в ряде др. математических задач. 1) Для решения уравнения

f ( x ) = 0 (1)

составляют ему равносильное х = j(х) , обозначив, например, через j(x) разность х — kf ( x ) ( k — постоянное). Выбрав a 0— начальное приближение к корню уравнения, составляют последовательность чисел a 0, a 1 = j( a 0 ) , a 2 = j( a 1 ) , …, a n = j( a n-1 ) , …; предел а = 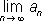, если он существует, является корнем уравнения (1), а числа a 0, a 1, a 2,..., a n,.. . — приближёнными значениями этого корня. Предел а будет существовать, например, если

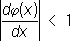(2)

и в качестве начального приближения a 0 взято любое число.

Обычно, когда надо найти приближённое значение корня уравнения, устанавливают достаточно узкий интервал, в котором лежит корень (например, с помощью графических методов); затем подбирают k так, чтобы условие (2) выполнялось на всём интервале; за начальное приближение a 0 выбирают любое число из этого интервала и применяют П. п. м. Практически, после того как два последовательных приближения a n-1 и a n совпадут с заданной степенью точности, вычисление прекращают и полагают a n » а. Пусть дано, например, уравнение f ( x ) = 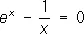. Так как , то корень уравнения лежит в интервале 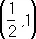. Положив 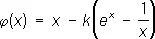, непосредственной проверкой убеждаемся, что для k = условие (2) выполняется на всём интервале 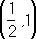. Выбирем a 0 = и применим П. п. м. к уравнению 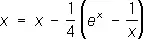. Получим a 1 = 0,554, a 2 = 0,570, a 3 = 0,566 (на самом деле корень уравнения с тремя верными десятичными знаками равен a 4 » 0,567).