БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

А. В. Иванов.

По'чковый долгоно'сик(Sciaphobus squalidis), жук семейства долгоносиков, опасный вредитель плодовых деревьев и ягодных кустарников, а также многих лесных лиственных пород. Тело длиной 5—7 мм густо покрыто чёрными чешуйками; надкрылья выпуклые яйцевидные, перепончатые крылья недоразвиты (П. д. не летает). Распространён в южных районах Европейской части СССР. Ранней весной перезимовавшие в почве неполовозрелые жуки объедают почки, листья, повреждают и бутоны; питаются только днём. Самка откладывает яйца на листья кучками по 10—40 штук, яйцекладка заканчивается в середине мая. Отрождающиеся личинки падают на землю и уходят в почву на глубине до 40—50 см; питаются корешками деревьев. В годы массового размножения П. д. наносят значительный ущерб урожаю. Меры борьбы: применение инсектицидов в период весеннего питания жуков.

По'чковый клещ сморо'дины[Eriophyes (Cecidophyopsis) ribis], галловый клещ; один из опаснейших вредителей чёрной и красной смородины в Европе. Тело (самок длина 0,2—0,22 мм, самцов — 0,18—0,20 мм ) червеобразное, на конце 2 хвостовые лопастевидные пластинки и 2 длинные щетинки. Питается тканями молодых почек. Быстро размножаясь, клещи вызывают галлообразное разрастание, разрыхление и засыхание почек или, реже, уродливое израстание их в виде пучка побегов. При сильном заражении урожай смородины резко снижается. П. к. с. переносит возбудителя вирусной махровости смородины. Меры борьбы: выращивание здоровых саженцев в специальных элитных маточниках и репродукционных питомниках, закладываемых термически обеззараженными черенками; ежегодная проверка, прочистка, обработка акарицидами и отбор лучших кустов для дальнейшего размножения; подбор более устойчивых к П. к. с. сортов.

Почку'ющиеся бакте'рии,группа бактерий, размножающихся почкованием. У обитающего в воде пресных и солёных водоёмов гетеротрофного микроорганизма Hyphomicrobium веретенообразная клетка (0,5´1—2 мкм ) даёт длинную, иногда ветвящуюся нить. На конце её образуется овальная почка со жгутиком на полюсе: отделившись от нити, почка перемещается в воде. К П. б. относится также фотосинтезирующий Rhodomicrobium, у которого почка, образующаяся на конце нити, имеет жгутики, расположенные по всей её поверхности. Размножение почкованием (наряду с делением и перешнуровыванием клеток) наблюдается не только у П. б., но и у родственных актиномицетам микобактерий.

По'чта[польск, poczta, от итал. posta, от позднелат. posita — остановка, станция (где меняли почтовых лошадей)], 1) пересылаемые предприятиями связи почтовые отправления: периодические издания, письменная корреспонденция, посылки, денежные переводы. 2) Предприятия связи, осуществляющие приём, пересылку, выдачу и доставку почтовых отправлений (почтамты, узлы связи, отделения перевозки П. по железной дороге, воздушным и водным линиям, а также отделения связи, входящие в состав почтамтов и узлов связи).

В широком смысле один из видов связи общего пользования (см. Почтовая связь ) .

«По'чта ду'хов»(в 18 в. произносилось — духо'в), ежемесячный журнал, издаваемый в Петербурге с января по август 1789. Издатель и, по-видимому, единственный автор — И. А. Крылов. Журнал был построен в виде переписки волшебника с духами; бытовые зарисовки чередовались здесь с морально-философскими рассуждениями. «П. д.» имела смелую политическую направленность, обличала не только нравственные пороки, но и общественные порядки самодержавно-крепостнической России.

Изд.: Крылов И. А., Соч., т. 1, М., 1945.

Лит.: Берков П. Н., «Почта духов» И. А. Крылова, в кн.: Труды юбилейной научной сессии ЛГУ. Секция филологических наук, Л., 1946; Благой Д, Д., Сатирическая проза Крылова, в кн.; И. А. Крылов. Исследования и материалы, М., 1947; Гордин А., Крылов в Петербурге, Л., 1969.

Почта'мт(от нем. Postamt), крупное предприятие связи, обслуживающее население, учреждения и предприятия всеми видами почтовой, телеграфной и телефонной связи. В СССР П. создаются в республиканских, краевых и областных центрах. Являясь центральным почтовым предприятием города, П. одновременно с выполнением производственных функций организует и направляет работу подчинённых ему отделений связи (см. Почтовая связь ) .

Почти' периоди'ческая фу'нкция, функция, значения которой при добавлении к аргументу надлежащим образом выбранных постоянных чисел (почти периодов) приближённо повторяются. Более точно: непрерывная функция f ( x ) , определённая для всех действительных значений х, называется почти периодической, если для каждого e > 0 можно указать такое l = l (e) , что в каждом интервале оси х длины l найдётся хотя бы одно число t = t(e), для которого при любом х выполняется неравенство | f ( x + t ) — f ( x )| < e. Числа t называются почти периодами функции f ( x ). Периодическая функции суть частные случаи П. п. ф.; простейшие примеры П. п. ф., не являющихся периодическими, получаются в результате сложения периодических функций с несоизмеримыми периодами, например cosx + cos 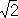x.

Некоторые наиболее важные свойства П. п. ф.:

1) П. п. ф. ограничена и равномерно непрерывна на всей оси х.

2) Сумма и произведение конечного числа П. п. ф. есть также П. п. ф.

3) Предел равномерно сходящейся последовательности П. п. ф. есть также П. п. ф.

4) Для каждой П. п. ф. существует среднее значение (на всей оси х ) :

.

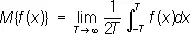5) Каждой П. п. ф. можно сопоставить ряд Фурье:

,

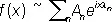причём l 1, l 2, …, l n, …, может быть любой последовательностью отличных друг от друга действительных чисел и

.

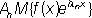6) Равенство Парсеваля: для каждой П. п. ф. справедливо равенство:

M {| f ( x )| 2} = .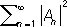

7) Теорема единственности: если f ( x ) есть непрерывная П. п. ф. и если для всех действительных l

М { f ( х ) е -i lx } = 0,

то f ( x ) º 0. Иначе говоря, ряд Фурье однозначно определяет П. п. ф.

8) Теорема аппроксимации: для каждого e > 0 можно указать такой конечный тригонометрический полином