БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

Геометрическое преобразование плоскости (или пространства), при котором все фигуры плоскости переходят в им подобные с одним и тем же коэффициентом П., называется подобным преобразованием. Подобное преобразование является частным случаем аффинного преобразования. Совокупность всех подобных преобразований плоскости (пространства) образует группу. Всякое подобное преобразование можно осуществить путём последовательного выполнения гомотетии и движения (собственного или несобственного).

П. и подобные преобразования применяются в моделировании, черчении и др. технических приложениях геометрии (см. также Пантограф ) .

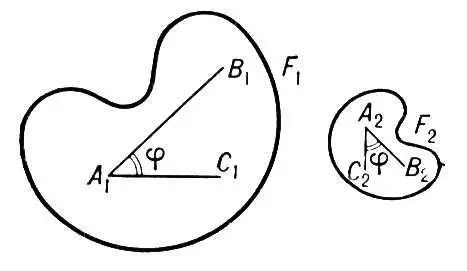
Рис. к ст. Подобие.

Подо'бие гидромехани'ческое, см. Подобия теория.

Подо'бия крите'рии, безразмерные (отвлечённые) числа, составленные из размерных физических параметров, определяющих рассматриваемые физические явления. Равенство всех однотипных П. к. для двух физических явлений и систем — необходимое и достаточное условие физического подобия этих систем. П. к., представляющие собой отношения одноимённых физических параметров системы (например, отношения длин), называются тривиальными и при установлении определяющих П. к. обычно не рассматриваются: равенство их для двух систем является определением физического подобия. Нетривиальные безразмерные комбинации, которые можно составить из определяющих параметров, и представляют собой П. к. Всякая новая комбинация из П. к. также является П. к., что дает возможность в каждом конкретном случае выбрать наиболее удобные и характерные критерии. Число определяющих нетривиальных П. к. меньше числа определяющих физических параметров с различными размерностями на величину, равную числу определяющих параметров с независимыми размерностями. Подробнее см. Подобия теория.

Если известны уравнения, описывающие рассматриваемое физическое явление, то П. к. для этого явления можно получить, приводя уравнения к безразмерному виду путём введения некоторых характерных значений для каждого из определяющих физических параметров, входящих в систему уравнений. Тогда П.к. определятся как безразмерные коэффициенты, появляющиеся перед некоторыми из членов новой, безразмерной системы уравнений. Когда уравнения, описывающие физическое явление, неизвестны, П. к. отыскиваются при помощи анализа размерностей, определяющих физические параметры (см. Размерностей анализ ) .

П. к. механического движения получается из уравнения, выражающего второй закон Ньютона и называется числом Ньютона Ne = Ft 2/ml, где F — действующая на тело сила, m — его масса, t — время, l — характерный линейный размер.

При изучении упругих деформаций конструкции под воздействием внешних сил основными П. к. являются Пуассона коэффициент для материала конструкции n= |e 1/e 2| и критерии r gl/E, F/El 2, где e = DL/L — относительная продольная деформация, e 1= D d/d — относительная поперечная деформация, Е — модуль Юнга, r — плотность материала конструкции, F — характерная внешняя сила, g — ускорение силы тяжести.

В гидромеханике важнейшими П. к. являются Рейнольдса числоRe = ru l/ m = u l/ m , Маха числоM = u /a * и Фруда числоFr = u 2/gl, где r — плотность жидкости или газа, u — скорость течения, m — динамический коэффициент вязкости, n = m/r — кинематический коэффициент вязкости, а * — местная скорость распространения звука в движущейся среде. Каждый из П. к. имеет определенный физический смысл как величина, пропорциональная отношению однотипных физических величин. Так, число Re характеризует отношение инерционных сил при движении жидкости или газа к силам вязкости, а число Fr — отношение инерционных сил к силам тяжести.

Основными П. к. процессов теплопередачи между жидкостью (газом) и обтекаемым телом являются Прандтля числоPr = n /а = m с р/ l , Нуссельта числоNu = al/ l , Грасгофа число Gr = b gl 3 D T/ n 2, а также Пекле числоPe = ul/a и Стэнтона числоSt = a /rc p u . Здесь a — коэффициент теплопередачи, l — коэффициент теплопроводности, c p— удельная теплоёмкость жидкости или газа при постоянном давлении, a = l / r c p— коэффициент температуропроводности, b — коэффициент объёмного расширения, D T — разность температур поверхности тела и жидкости (газа). Два последних числа связаны с предыдущими соотношениями: Ре = Pr × Re, St = Nu/Pe.

Для распространения тепла в твёрдом теле характерны П. к.: Фурье числоFo = at/l 2 и число Био Bi = a l/ l . Число Bi определяет характер соответствия между температурными условиями в окружающей среде и распределением температуры в теле.

В процессах, изменяющихся с течением времени t, основным критерием подобия, характеризующим одинаковость протекания процессов во времени, является критерий гомохронности Ho = ut/l. В задачах гидроаэромеханики нестационарных течений этот критерий обычно называется Струхаля числомSh. Критерий гомохронности в случае подобия электродинамических явлений записывают в виде Ho = wt, где w — характерная частота.

Примером П. к. электромагнитных полей служат критерии: mg l 2/t и e/g t, где m — магнитная проницаемость среды, g — её удельная проводимость, e — диэлектрическая проницаемость среды, а в случае подобия электрических цепей с распределёнными параметрами — критерии: L/Rt и C/Gt, где L — индуктивность, R — сопротивление, С — ёмкость, G — проводимость.

Лит. см. при ст. Подобия теория.

С. Л. Вишневецкий, С. М. Тарг.

Подо'бия тео'рия, учение об условиях подобия физических явлений. П. т. опирается на учение о размерностях физических величин (см. Размерностей анализ ) и служит основой моделирования физического. Предметом П. т. является установление подобия критериев различных физических явлений и изучение с помощью этих критериев свойств самих явлений.

Физические явления, процессы или системы подобны, если в сходственные моменты времени в сходственных точках пространства значения переменных величин, характеризующих состояние одной системы, пропорциональны соответствующим величинам другой системы. Коэффициенты пропорциональности для каждой из величин называется коэффициентом подобия.

Физическое подобие является обобщением элементарного и наглядного понятия геометрического подобия. При геометрическом подобии существует пропорциональность (подобие) сходственных геометрических элементов подобных фигур или тел. При физическом подобии поля соответствующих физических параметров двух систем подобны в пространстве и времени. Например, при кинематическом подобии существует подобие полей скорости для двух рассматриваемых движений; при динамическом подобии реализуется подобие систем действующих сил или силовых полей различной физической природы (силы тяжести, силы давления, силы вязкости и т.п.); механическое подобие (например, подобие двух потоков жидкости или газа, подобие двух упругих систем и т.п.) предполагает наличие геометрического, кинематического и динамического подобий; при подобии тепловых процессов подобны соответствующие поля температур и тепловых потоков; при электродинамическом подобии — поля токов, нагрузок, мощностей, поля электромагнитных сил. Все перечисленные виды подобия — частные случаи физического подобия.