БСЭ БСЭ - Большая Советская Энциклопедия (РА)

Лит.: Толмачев А, И., Введение в географию растений, Л., 1974.

А. И. Толмачев.

«Рассе'рженные молоды'е лю'ди»,или «Сердитые молодые люди» («Angry young men»), принятое в критике название группы английских писателей, выступивших в 50-е гг. 20 в. Термин восходит к автобиографической книге Л. А. Пола «Рассерженный молодой человек» (1951); широко распространился после постановки в Лондоне в 1956 пьесы Дж. Осборна «Оглянись во гневе» — в страстных мизантропических монологах её героя дана концентрация настроений «Р. м. л.». Наиболее типичные «Р. м. л.» — романисты Дж. Уэйн, К. Эмис, Дж. Брейн и драматург Осборн, которые, однако, не образовали литературной школы. «Р. м. л.» объединяет недовольство английской буржуазной действительностью и, в частности, положением молодёжи в обществе, протест против социального неравенства, сословного чванства, лжи и лицемерия. Их герой — обычно молодой человек, получивший университетское образование; он разочарован в жизни, недоволен своей работой, обществом, в котором ему нет места. Бунт против принятых норм поведения и морали он проявляет в экстравагантных и шутовских выходках, в скандальном адюльтере, в демонстративном уходе в ряды рабочего класса. «Р. м. л.» не выдвинули положительной программы, их критика носила индивидуалистический характер. К концу 50-х гг. они отошли от прежних тем и героев.

Лит.: Ивашева В. В., Английская литература XX века, М., 1967; Гозенпуд А. А., Пути и перепутья, Л., 1967; Шестаков Д., Современная английская драма (Осборновцы), М., 1968; Maschler Т. (ed.), Declaration, by С. Wilson [and others], L., 1957; Allsop K., The angry decade, L., 1958; Gindin J., Postwar British fiction, Berk., 1962.

Рассея'ние микрочасти'ц,теория рассеяния, процесс столкновения частиц, в результате которого меняются импульсы частиц (упругое рассеяние) или наряду с изменением импульсов меняются также их внутреннего состояния либо образуются др. частицы (неупругое рассеяние).

Одна из основных количественных характеристик как упругого рассеяния, так и неупругих процессов, — эффективное поперечное сечение процесса (называемое обычно просто сечением) — величина, пропорциональная вероятности процесса и имеющая размерность площади ( см 2). Измерение сечений процессов позволяет изучать законы взаимодействия частиц, исследовать структуру частиц. Например, классическими опытами Э. Резерфорда по рассеянию a-частиц атомами было установлено существование атомных ядер (см. Резерфорда формула ); из опытов по рассеянию электронов большой энергии на протонах и нейтронах (нуклонах) получают информацию о структуре нуклонов; эксперименты по упругому рассеянию нейтронов и протонов протонами позволяют детально исследовать ядерные силы и т.д. (О столкновениях атомов и ядер см. Столкновения атомные , Ядерные реакции. )

Классическая теория рассеяния.Согласно законам классической (нерелятивистской) механики, задачу рассеяния двух частиц с массами m 1и m 2можно свести переходом к системе центра инерции сталкивающихся частиц (системе, в которой покоится центр инерции частиц, т. е. суммарный импульс частиц равен нулю) к задаче рассеяния одной частицы с приведённой массой m = m 1 m 2/( m 1+ m 2) на неподвижном силовом центре. В силовом поле (с центром О ) траектория частицы искривляется — происходит рассеяние. Угол между начальным ( р нач) и конечным ( р кон) импульсами рассеиваемой частицы называется углом рассеяния. Угол рассеяния J зависит от взаимодействия между частицами и от т. н. прицельного параметра r — расстояния, на котором частица пролетела бы от силового центра, если бы взаимодействие отсутствовало ( рис. 1 ). Классическая механика устанавливает следующую связь между прицельным параметром и углом рассеяния:

,

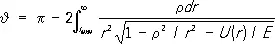где U ( r ) — потенциальная энергия взаимодействия, r — расстояние до силового центра ( r мин— минимальное расстояние), Е = р 2 нач/2m — энергия частицы.

На опыте обычно не измеряют рассеяние индивидуальной частицы, а направляют на мишень из исследуемого вещества пучок одинаковых частиц, имеющих одинаковую энергию, и измеряют количество частиц, рассеянных под данным углом. Число частиц dN , рассеянных в единицу времени на углы, лежащие в интервале J, J + d J, равно числу частиц, проходящих в единицу времени через кольцо 2pr d r× n. Если n — плотность потока падающих частиц (число частиц, проходящих в единицу времени через единичную площадку, перпендикулярную направлению движения частиц в пучке), то dN = 2pr d r× n, а сечение упругого рассеяния d s определяется как отношение dN /n и равно

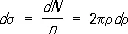(2)

(т. е., как уже отмечалось, сечение имеет размерность площади). Сечение рассеяния на все углы — полное сечение рассеяния — получается интегрированием (2) по всем прицельным параметрам. Если а — минимальный прицельный параметр, при котором J = 0 (т. е. частица проходит без отклонения), то полное сечение рассеяния s = p a 2 .

Квантовая теория рассеяния.В квантовой теории процессы упругого рассеяния и неупругие процессы описываются амплитудами рассеяния — комплексными величинами, квадрат модуля которых пропорционален сечениям соответствующих процессов. В 1943 В. Гейзенберг для описания процессов рассеяния ввёл т. н. S -матрицу, или матрицу рассеяния. Её матричные элементы определяют амплитуды различных процессов. Через матричные элементы S -матрицы выражаются физические величины, непосредственно измеряемые на опыте: сечение, поляризация частиц (среднее значение оператора спина), асимметрия, возникающая при рассеянии на поляризованной мишени и др. С др. стороны, матричные элементы S -матрицы могут быть вычислены при определённых предположениях о виде взаимодействия. Сравнение результатов опыта с предсказаниями теории позволяет проверить теорию.

Общие принципы инвариантности (инвариантность относительно вращений, из которой вытекает сохранение момента количества движения, отражений — сохранение чёткости, обращения времени и др.) существенно ограничивают возможный вид матричных элементов S -матрицы и позволяют получить проверяемые на опыте соотношения. Например, из закона сохранения чётности следует, что поляризация конечной частицы при столкновении неполяризованных частиц направлена по нормали к плоскости рассеяния (плоскости, проходящей через начальный и конечный импульсы частицы). Измеряя направление вектора поляризации, можно выяснить, сохраняется ли чётность во взаимодействии, обусловливающем процесс. Изотопическая инвариантность сильных взаимодействий приводит к соотношениям между сечениями различных процессов, а также к запрету некоторых процессов. В частности, из изотопической инвариантности следует, что при столкновении двух дейтронов не могут образоваться a-частица и p°-мезон. Исследование этого процесса на опыте подтвердило справедливость изотопической инвариантности.