БСЭ БСЭ - Большая Советская Энциклопедия (РА)

Условие унитарности S -матрицы, являющееся следствием сохранения полной вероятности (суммарная вероятность рассеяния по всем возможным каналам реакции должна равняться 1), также накладывает ограничения на матричные элементы процессов. Одно из важных соотношений, вытекающих из этого условия, — оптическая теорема , связывающая амплитуду упругого рассеяния на угол 0° с полным сечением (суммой сечений упругого рассеяния и сечений всех возможных неупругих процессов).

Из общих принципов квантовой теории ( микропричинности условия , релятивистской инвариантности и др.) следует, что матричные элементы S -матрицы являются аналитическими функциями в некоторых областях комплексных переменных. Аналитические свойства матричных элементов S -матрицы позволяют получить ряд соотношений между определяемыми из опыта величинами — т. н. дисперсионные соотношения (см. Сильные взаимодействия ), Померанчука теорему и др.

В случае упругого рассеяния бесспиновых частиц асимптотика волновой функции Y( r ), являющейся решением Шрёдингера уравнения, имеет вид:

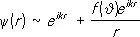(3)

Здесь r — расстояние между частицами, k = p/ 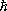— волновой вектор, р — импульс в системе центра инерции (с. ц. и.) сталкивающихся частиц, 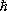— постоянная Планка, J — угол рассеяния, f (J) — амплитуда рассеяния, зависящая от угла рассеяния и энергии сталкивающихся частиц. Первый член в этом выражении описывает свободные частицы с импульсом р = 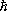k (падающая волна), второй — частицы, идущие от центра (рассеянная волна). Дифференциальное сечение рассеяния определяется как отношение числа частиц, рассеянных за единицу времени в элемент телесного угла d W, к плотности потока падающих частиц. Сечение рассеяния на угол J (в с. ц. и.) в единичный телесный угол равно:

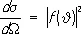(4)

Для амплитуды рассеяния имеет место следующее разложение по парциальным волнам (волнам с определённым орбитальным моментом l ):

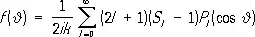(5)

Здесь P l (cosJ) — Лежандра многочлен, S l — коэффициенты разложения, которые зависят от характера взаимодействия и являются матричными элементами S -матрицы (в представлении, в котором она диагональна по энергии, моменту количества движения и проекции момента). Если число падающих на центр частиц с моментом l равно числу идущих от центра частиц с тем же моментом (случай упругого рассеяния), то I S l l = 1. В общем случае l S l l £ 1. Эти условия являются следствием условия унитарности S -матрицы. Если возможно только упругое рассеяние, то S lможет быть представлено в виде: S l= e 2i d l , где d l— вещественные величины, называемые фазами рассеяния. Если d l= 0 при некотором l , то рассеяние в состояние с орбитальным моментом l отсутствует.

Полное сечение упругого рассеяния равно:

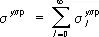(6)

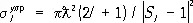
где 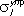; — парциальное сечение упругого рассеяния частиц с орбитальным моментом l , 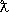= 1/ k — длина волны де Бройля частицы. При Sl = —1 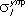достигает максимума и равно:

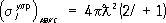(7)

при этом d l= p/2 (резонанс в рассеянии). Т. о., при резонансе сечение процесса определяется де-бройлевской длиной волны 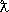и для медленных частиц, для которых 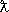>> R 0 , где R 0 — радиус действия сил, намного превосходит величину p R 0 2(классическое сечение рассеяния). Этот факт (непонятный с точки зрения классической теории рассеяния) является следствием волновой природы микрочастиц.

Поведение сечения рассеяния вблизи резонанса определяется формулой Брейта — Вигнера:

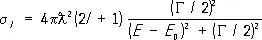, (8)

где E 0 — энергия, при которой сечение достигает максимума (положение резонанса), а Г— ширина резонанса. При Е = E 0± 1/ 2G сечение s lравно 1/ 2 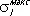. Полное сечение всех неупругих процессов равно:

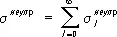(9)

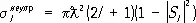
Условие унитарности ограничивает величину парциального сечения для неупругих процессов:

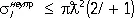. (10)

Для короткодействующих потенциалов взаимодействия основную роль играют фазы рассеяния с l £ b / k, где b — радиус действия сил. Это условие можно переписать следующим образом: l / k £ b ; величина l / k определяет минимальное расстояние, на которое может приблизиться к центру сил свободная частица с моментом l (прицельный параметр в квантовой теории). При bk << 1 (малые энергии) следует учитывать только S -волну (парциальную волну с l = 0). Амплитуда рассеяния в этом случае равна:

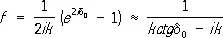(11)

и сечение рассеяния не зависит от угла (рассеяние сферически симметрично). При малых энергиях имеет место разложение:

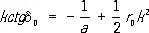(12)

Параметры а и r 0 называются соответственно длиной рассеяния и эффективным радиусом рассеяния. Эти величины определяются из опыта и являются важными характеристиками сил, действующих между частицами. Длина рассеяния равна по величине и противоположна по знаку амплитуде рассеяния при k = 0. Полное сечение рассеяния в точке k = 0 равно s 0= 4p a 2 .