БСЭ БСЭ - Большая Советская Энциклопедия (РА)

Поскольку поперечные размеры Р. сравнимы с l, то задача о распространении и возбуждении в них электромагнитного поля решается на основе интегрирования Максвелла уравнений при заданных граничных условиях и источниках поля. Методы решения этих задач составляют содержание теории Р. В случае прямоугольного Р. ( рис. 3 ) для любой из проекций f электрического Е и магнитного Н полей теория приводит к волновому уравнению:

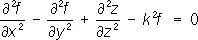(1)

где k = 2p/l = w/с — волновое число, w — частота колебаний, с — скорость света. Решение этого уравнения для бесконечно длинного прямоугольного Р. приводит к следующим выражениям для комплексных амплитуд проекций векторов Е и Н:

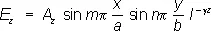(2)

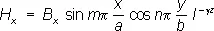
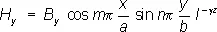
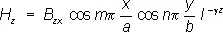
Здесь а и b — размеры поперечного сечения прямоугольного Р., m и n — любые положительные целые числа, A x , A yA z , B x , B y , B z— постоянные определяемые условиями возбуждения Р. Постоянная распространения g, определённая из (2) и (1), равна:

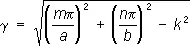(3)

Наличие тригонометрических множителей в (2) говорит об образовании стоячих волн в направлениях, перпендикулярных стенкам Р. Касательные составляющие электрического поля на стенках имеют узлы, а нормальные — пучности. Числа m и n определяют число полуволн, укладывающихся соответственно вдоль размеров а и b. Чем больше m и n , тем сложнее поле в сечении Р.

В Р. волновое поле является суммой полей бесконечного множества типов волн. Все типы волн подразделяются на три класса: ТЕ (или Н )-волны, ТМ (или Е ) - волны и ТЕМ -волны; Т означает поперечность (трансверсальность). Каждый тип волн имеет свою структуру поля: в ТЕ -волнах электрическое поле сводится лишь к поперечным составляющим, но магнитное поле имеет и продольную, и поперечную составляющие; ТМ -волны имеют только поперечные составляющие магнитного поля; продольную составляющую имеет лишь электрическое поле; ТЕМ- волны вообще не имеют продольных составляющих поля и могут существовать только в многосвязных Р. Волны с различными m и n записываются в виде TMmn и TEmn (или Emn , Hmn ). Волны с наименьшими индексами m и n называются простейшими. В случае ТМ -волн ( H z = 0) простейшей волной является волна ТМ 11( рис. 4 ).

Волны TM 10и TM 01неосуществимы, т.к. магнитные силовые линии должны быть замкнутыми. Более сложные волны возникают, если увеличить поперечные размеры Р. или частоту колебаний так, чтобы вдоль размеров а и b укладывалась более чем одна полуволна. При этом поперечное сечение Р., подобно колеблющейся мембране, оказывается разбитым на ячейки, тождественные по структуре поперечному сечению волны ТМ 11( рис. 5 ).

В случае ТЕ -волн ( Е 32= 0) возможно существование волн при m = 0, n ¹ 0 или n = 0, m ¹ 0, т.к. линии электрического поля могут быть прямыми, начинающимися на противоположных стенках Р. ( рис. 6 , 7 ). Из волн TE 10и ТЕ 11как из ячеек, составляются все сложные типы ТЕ- волн ( рис. 8 ).

Множитель е - gzопределяет изменения амплитуды и фазы волны при распространении её вдоль оси Р. При отсутствии потерь должна быть чисто мнимой величиной: g = i a, т. е. 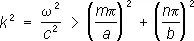. Это соответствует условию для частоты:

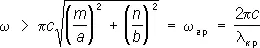
которое означает, что Р. пропускает без затухания только колебания с частотой выше некоторой граничной частоты w гр ; ей соответствует критическая длина волны l кр. Граничная частота w гртем выше, чем меньше а и b, т. е. размеры Р. При заданной рабочей частоте w нужны тем большие размеры Р. а и b , чем больше m и n , т. е. чем сложнее волна.

Длина волны в Р. Л оказывается большей, чем в свободном пространстве:

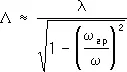. (5)

Фазовая скорость распространения волны в Р. равна:

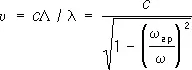, (5a),

т. е. всегда больше скорости света и зависит от частоты колебаний. Это означает, что в Р. имеет место дисперсия волн , вносящая искажения в передаваемые сигналы тем больше, чем шире спектр их частот.

Затухание волны в Р. описывается вещественной частью комплексной постоянной распространения g = b + i a и объясняется в реальных Р. потерями в стенках и в заполняющем Р. диэлектрике. В «идеальных» (без потерь) Р., если w < w гр, электромагнитное поле затухает без потерь энергии (за счёт полного отражения). В Р. можно работать только на одном первом типе волны, выбрав размеры Р. определённым образом (например, для прямоугольного Р. и волны H 10), выбрав величину а из соотношения a < l < 2 а ). Обычно берут а = 0,72 см , что даёт: а = 72 мм на l = 10 см ; a = 23 мм на l = 3,2 см (см. табл.).

Совокупность двух классов волн магнитного и электрического типов в каждом Р. образует полную систему волн. Это означает, что в Р. могут распространяться электромагнитные поля только таких структур, которые могут быть представлены как результат суперпозиции воли магнитного и электрического типов.

Для Р. круглых сечений основным уравнением вместо (1) становится Бесселя уравнение с решениями в виде цилиндрических функций. В круглом Р. также можно выбрать диаметр Р. для работы только на одном первом типе волны (см. табл.). Однако не всегда первый тип волны оказывается наиболее удобным. Например, в силу осевой симметрии полей у волн ТМ 01и TE 01в круглом Р. ( рис. 9 , 10 ) эти волны применяют во вращающихся соединениях. На рис. 11 и 12 показаны структуры поля волн TM 11и ТЕ 11в круглом Р. Применение волн с относительно малым l крзатруднительно, т.к. при обеспечении условий распространения для них одновременно в Р. будут распространяться и все предыдущие «ненужные» типы волн.