БСЭ БСЭ - Большая Советская Энциклопедия (РИ)

Решением этих уравнений являются числа a 1 = 71/369 и a 2 = 7/ 41 . Следовательно, 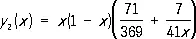. Полученное приближённое решение отличается от точного на величину порядка 0,001.

Найденное этим методом приближённое решение у п ( х ) вариационной задачи при некоторых условиях, касающихся в основном полноты системы функций j i ( x ) , стремится к точному решению у ( х ) , когда n ® ¥.

Метод был предложен в 1908 немецким математиком В. Ритцем (W. Ritz). Теоретическое обоснование метода дано сов. математиком Н. М. Крыловым (1918).

Метод Галёркина является широким обобщением метода Ритца и применяется главным образом для приближённого решения вариационных и краевых задач, в том числе и тех, которые не сводятся к вариационным. Основная идея метода Галёркина состоит в следующем. Пусть требуется в некоторой области D найти решение дифференциального уравнения

L [ u ] = 0 (1)

(L — некоторый дифференциальный оператор, например по двум переменным), удовлетворяющее на границе S области D однородным краевым условиям:

u = 0. (2)

Если функция u является решением уравнения (1) в области D, то функция L [ u ] тождественно равна нулю в этой области и, следовательно, ортогональна (см. Ортогональность ) любой функции в области D. Приближённое решение уравнения (1) ищут в виде

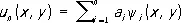, (3)

где y i ( x, y ) ( i = 1, 2,..., n ) — линейно независимые функции, удовлетворяющие краевым условиям (2) и являющиеся первыми n функциями некоторой системы функций y 1 ( x, у ) , y 2 ( х, у ) ,..., y п ( х, у ) ,..., полной в данной области. Постоянные коэффициенты a i выбирают так, чтобы функция L [ u n ] была ортогональна в D первым n функциям системы y i ( x, y ):

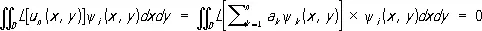(4)

.

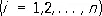Например, пусть в области D требуется решить уравнение Пуассона

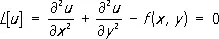
при условии u = 0 на S . Выбирая систему функций y i ( x, y ) , ищем решение в виде (3). Система уравнений (4) для определения коэффициентов ai имеет вид:

.

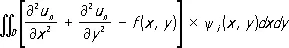
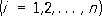Функции y i ( x, y ) можно, в частности, выбирать, пользуясь следующими соображениями. Пусть w( x, y ) — непрерывная функция, имеющая внутри области D непрерывные частные производные второго порядка и такая, что w( x, y ) > 0 внутри D, w( x, y ) = 0 на S . Тогда в качестве системы функций y i ( x, y ) можно взять систему, составленную из произведений w( x, y ) на различные степени х и y : 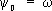, , 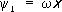, , 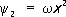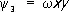… Например, если границей области D является окружность S радиуса R с центром в начале координат, то можно положить w( x, y ) = R 2— x 2— y 2.

Метод Галёркина применяется при решении широкого класса задач; более общая его формулировка даётся в терминах функционального анализа для решения уравнений вида Au — f = 0, где А — линейный оператор, определённый на линеале, плотном в некотором гильбертовом пространстве H, u — искомый и f — заданный элементы пространства H.

Метод получил распространение после исследований Б. Г. Галёркина (1915); ранее (1913) он применялся для решения конкретных задач теории упругости И. Г. Бубновым, в связи с чем иногда именуется методом Бубнова — Галёркина. Теоретическое обоснование метода принадлежит М. В. Келдышу (1942).

Лит.: Галёркин Б. Г., Стержни и пластинки. Ряды в некоторых вопросах упругого равновесия стержней и пластинок, «Вестник инженеров», 1915, т. 1, № 19, с. 897—908; Михлин С. Г., Вариационные методы в математической физике, 2 изд., М. — Л., 1970; Канторович Л. В. и Крылов В. И., Приближённые методы высшего анализа, 5 изд., Л. — М., 1962; Ritz W., Neue Methode zur Lösung gewisser Randwertaufgaben, «Gesellschaft der Wissenschaften zu Göttingen. Math.-physik. Klasse. Nachrichten», Göttingen, 1908; его же, Über еще neue Methode zur Lösung gewisser Variationsprobleme der mathematischen Physik, «Journal für die reine und angewandte Mathematik», 1909, Bd 135.

В. Г. Карманов.

Ри'у-Бра'нку(Rio Branco), река в Бразилии, левый приток Риу-Негру (бассейн Амазонки). Образуется слиянием рр. Урарикая и Такуту. Длина её с р. Урарикая, берущей начало на восточных склонах хребта Серра-Парима под названием Парима, 1300 км, площадь бассейна около 195 тыс. км 2. Река течёт по Гвианскому плоскогорью и Амазонской низменности. Летние (июнь, июль) паводки. Средний расход воды около 5400 м 3/сек. Судоходна до селения Каракараи, в высокую воду — до г. Боа-Виста.

Ри'у-Гра'нди(Rio Grande), город на Ю.-В. Бразилии, в штате Риу-Гранди-ду-Сул. 116,8 тыс. жителей (1970, с пригородами). Ж.-д. станция Порту входа в озеро-лагуну Патус (ошибочно принятое португальцами за большую реку, откуда и название города); грузооборот 3,1 млн. т (1971), вывоз риса, мясопродуктов, шерсти, кожсырья. Пищевая (мясо- и рыбоконсервная, пивоваренная и др.), табачная, кожевенно-обувная, химическая промышленность. Основан в 1737.

Ри'у-Гра'нди(Rio Grande), река на Ю.-В. Бразилии, левая составляющая реки Параны. Длина 1230 км, площадь бассейна 170 тыс. км 2. Берёт начало близ Атлантического побережья в горах Серра-да-Мантикейра, течёт по Бразильскому плоскогорью, образуя несколько водопадов. Питание дождевое, многоводна в январе — марте. Средний расход воды 2000 м 3/сек. В верхнем течении крупное водохранилище Фурнас объёмом 20,2 км 3 и ГЭС мощностью 1,2 Гвт. Р.-Г. местами судоходна.

Ри'у-Гра'нди-ду-Ни'рти(Rio Grande do Norte), штат на С.-В. Бразилии. Площадь 53 тыс. км 2. Население 1,6 млн. чел. (1970). Административный центр — г. Натал. Основа экономики — отсталое сельское хозяйство. На побережье Атлантического океана выращивают сахарный тростник, на З. — длинноволокнистый хлопчатник, на Ю. — сизаль (около 30% общенационального сбора). Сбор воска карнаубской пальмы (2-е место в стране). Добывают вольфрам, поваренную соль. Переработка с.-х. сырья.