БСЭ БСЭ - Большая Советская Энциклопедия (РЕ)

Лит.: Власов В. Ф., Электронные и ионные приборы, 3 изд., М., 1960.

Резо'лы,резольные смолы, термореактивные продукты поликонденсации фенолов с альдегидами (главным образом формальдегидом) невысокой молекулярной массы (400—1000). Р. — вязкие жидкости или твёрдые продукты от светло-жёлтого до чёрного цвета. Содержат в макромолекулах реакционноспособные метилольные (—СН 2ОН) группы. См. Феноло-альдегидные смолы.

Резольве'нта(лат. resolvens, родительный падеж resolventis — развязывающий, решающий, от resolvo — развязываю, решаю) (математическая), разрешающее уравнение, разрешающая функция (ядро) или разрешающие операторы.

В алгебре термин «Р.» употребляется в нескольких смыслах. Так, под Р. алгебраического уравнения f ( x ) = 0 степени n понимают такое алгебраическое уравнение g ( x ) = 0 с коэффициентами, рационально зависящими от коэффициентов f ( x ), что знание корней этого уравнения позволяет найти корни данного уравнения f ( x ) = 0 в результате решения более простых уравнений, степеней не больших n. Например, уравнение

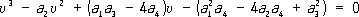
является одной из (кубической) Р. уравнения четвёртой степени

x 4+ a 1 x 3+ a 2 x 2+ a 3 x + a 4= 0. (1)

Если u 1, u 2, u 3— корни этой Р., то корни x 1, x 2, x 3, x 4уравнения (1) могут быть найдены решением квадратных уравнений s 2 — u ks + a 4= 0, k = 1, 2, 3. Именно, если x k, h k — корни этих квадратных уравнений, то x 1 x 2 = x 1, x 3 x 4 = h 1, x 1 x 3 = x 2, x 2 x 4 = h 2, x 1 x 4= x 3, x 2 x 3 = h 3и x 1 2 = x 1x 2/h 3и т. д. Резольвентой Галуа уравнения f ( x ) = 0 называется такое неприводимое над данным полем алгебраическое уравнение g ( x ) = 0 (см. Галуа теория ), что в результате присоединения одного из его корней к этому полю получается поле, содержащее все корни уравнения f ( x ) = 0.

В несколько ином смысле термин «Р.» употребляется в т. н. проблеме резольвент Гильберта и Чеботарева.

В теории интегральных уравнений под Р. (разрешающим ядром) уравнения

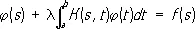(2)

понимают функцию Г( х , t , l) переменных s , t и параметра l, при помощи которой решение уравнения (2) представляют в виде

,

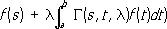если l не есть собственное значение уравнения (2), например для ядра К ( s , t ) = s + t резольвентой является функция

G (s, t ; l) =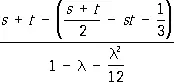

В теории линейных операторов под Р. оператора А понимают семейство операторов R l= ( А — l E ) -1, где комплексный параметр l принимает любые значения, не принадлежащие спектру оператора А.

Резольво'метр(от лат. resolvo — развязываю, вскрываю, распутываю и ...метр ), прибор для измерения разрешающей способности (РС) фотоматериалов. Наиболее распространены проекционные Р., в которых на фотоматериал через микроскопический объектив при обратном ходе лучей света проецируют уменьшенные изображения штриховой миры (обычно с П-образным распределением яркости вдоль решётки). Ряд таких изображений, полученных при различных строго отмеренных экспозициях , образует на фотоматериале резольвограмму; РС материала и её зависимость от экспозиции определяют, рассматривая поля резольвограммы под микроскопом. Измеренное значение РС зависит от апертуры объектива, достигая наибольшей величины при апертурах ~ 0,2—0,3; поэтому объективы проекционных Р. имеют определённые апертуры. Контраст фотографический изображений миры в проекционном Р. уменьшается с увеличением частоты её штрихов. Напротив, в интерференционных Р., применяемых для исследования особо высокоразрешающих материалов (например, используемых в голографии ), контраст не зависит от частоты интерференционных полос, запечатлеваемых в фотослое: их яркость меняется вдоль решётки синусоидально. Пространственную частоту полос можно менять перемещениями оптических деталей создающего интерференционную картину интерферометра.

Лит. см. при ст. Разрешающая способность фотографирующей системы.

М. Я. Шульман.

Резолю'ция(от лат. resolutio — решение), 1) решение, принятое в результате обсуждения какого-либо вопроса на заседании (съезде, конференции, сессии) коллегиального органа, собрания и т. п. 2) Надпись на документе, сделанная должностным лицом и содержащая принятое им решение.

Резонё р(франц. raisonneur, от raisonner — рассуждать) (устаревшее), сценическое амплуа: актёр, исполняющий роли рассудочных людей, склонных к риторическим декларациям, назидательным сентенциям. Р. обычно высказывает мысли автора по поводу изображаемых событий, даёт моральные оценки поступкам других действующих лиц. Наибольшее распространение роли Р. получили в европейском театре 17—18 вв. (Клеант — «Тартюф» Мольера, Стародум — «Недоросль» Фонвизина, и др.).

Резона'нс(франц. resonance, от лат. resono — звучу в ответ, откликаюсь), явление резкого возрастания амплитуды вынужденных колебаний в какой-либо колебательной системе , наступающее при приближении частоты периодического внешнего воздействия к некоторым значениям, определяемым свойствами самой системы. В простейших случаях Р. наступает при приближении частоты внешнего воздействия к одной из тех частот, с которыми происходят собственные колебания в системе, возникающие в результате начального толчка. Характер явления Р. существенно зависит от свойств колебательной системы. Наиболее просто Р. протекает в тех случаях, когда периодическому воздействию подвергается система с параметрами, не зависящими от состояния самой системы (т. н. линейные системы ).

Типичные черты Р. можно выяснить, рассматривая случай гармонического воздействия на систему с одной степенью свободы: например, на массу m , подвешенную на пружине, находящуюся под действием гармонической силы F = F 0coswt ( рис. 1 ), или электрическую цепь, состоящую из последовательно соединённых индуктивности L , ёмкости С , сопротивления R и источника электродвижущей силы Е , меняющейся по гармоническому закону ( рис. 2 ). Для определенности в дальнейшем рассматривается первая из этих моделей, но всё сказанное ниже можно распространить и на вторую модель. Примем, что пружина подчиняется закону Гука (это предположение необходимо, чтобы система была линейна), т. е., что сила, действующая со стороны пружины на массу m , равна kx , где х — смещение массы от положения равновесия, k — коэффициент упругости (сила тяжести для простоты не принимается во внимание). Далее, пусть при движении масса испытывает со стороны окружающей среды сопротивление, пропорциональное её скорости 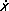и коэффициенту трения b , т. е. равное k 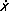(это необходимо, чтобы система оставалась линейной). Тогда уравнение движения массы m при наличии гармонической внешней силы F имеет вид: