БСЭ БСЭ - Большая Советская Энциклопедия (СТ)

В. М. Симчера.

Статисти'ческий ана'лиз многоме'рный,в широком смысле — раздел математической статистики , объединяющий методы изучения статистических данных, относящихся к объектам, которые характеризуются несколькими качественными или количественными признаками. Наиболее разработана часть С. а. м., основанная на допущении, что результаты отдельных наблюдений независимы и подчинены одному и тому же многомерному нормальному распределению (обычно именно к этой части применяют термин С. а. м. в узком смысле). Иными словами, результат X j наблюдения с номером j можно представить вектором

X j= ( X j1, X j2,..., X js ),

где случайные величины X jk имеют математическое ожидание m k , дисперсию s 2 k , а коэффициент корреляции между X jk и X jl равен r kl . Вектор математических ожиданий m = (m 1,..., m s ) и ковариационная матрица S с элементами s k s l r kl, k, l = 1 ,..., s , являются основными параметрами, полностью определяющими распределение векторов X 1 ,..., X n — результатов п независимых наблюдений. Выбор многомерного нормального распределения в качестве основной математической модели С. а. м. отчасти может быть оправдан следующими соображениями: с одной стороны, эта модель приемлема для большого числа приложений, с другой — только в рамках этой модели удаётся вычислить точные распределения выборочных характеристик. Выборочное среднее 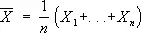и выборочная ковариационная матрица

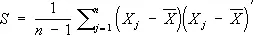
[где 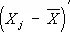обозначает транспонированный вектор 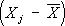, см. Матрица ] суть оценки максимального правдоподобия соответствующих параметров совокупности. Распределение 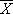нормально 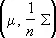, а совместное распределение элементов ковариационной матрицы S , т. н. распределение Уишарта, является естественным обобщением «хи-квадрат» распределения и играет значительную роль в С. а. м.

Ряд задач С. а. м. более или менее аналогичен соответствующим одномерным задачам (например, задача проверки гипотез о равенстве средних значений в двух независимых выборках). Другого типа задачи связаны с проверкой гипотез о независимости тех или иных групп компонент векторов X j ,проверкой таких специальных гипотез, как гипотеза сферической симметрии распределения X j и т.д. Необходимость разобраться в сложных взаимосвязях между компонентами случайных векторов X j ставит новые проблемы. В целях сокращения числа рассматриваемых случайных признаков (уменьшения размерности) или сведения их к независимым случайным величинам применяются метод главных компонент и метод канонических корреляций. В теории главных компонент осуществляется переход от векторов Xj к векторам Y j= ( Y j1,..., Y jr ). При этом, например, Y j1 выделяется максимальной дисперсией среди всех нормированных линейных комбинаций компонент X 1 ; Y j2 имеет наибольшую дисперсию среди всех линейных функций компонент X 1 , не коррелированных с Y j1 и т.д. В теории канонических корреляций каждое из двух множеств случайных величин (компонент X j ) линейно преобразуется в новое множество т. н. канонических величин так, что внутри каждого множества коэффициенты корреляции между величинами равны 0, первые координаты каждого множества имеют максимальную корреляцию, вторые координаты имеют наибольшую корреляцию из оставшихся координат и т.д. (упорядоченные т. о. корреляции называются каноническими). Последний метод указывает максимальную корреляцию линейных функций от двух групп случайных компонент вектора наблюдения. Выводы методов главных компонент и канонических корреляций помогают понять структуру изучаемой многомерной совокупности. Сходным целям служит и факторный анализ , в схеме которого предполагается, что компоненты случайных векторов X j явлются линейными функциями от некоторых ненаблюдаемых факторов, подлежащих изучению. В рамках С. а. м. рассматривается и проблема дифференциации двух или большего числа совокупностей по результатам наблюдений. Одна часть проблемы заключается в том, чтобы на основе анализа выборок из нескольких совокупностей отнести новый элемент к одной из них (дискриминация), другая — в том, чтобы внутри совокупности разделить элементы на группы, в определённом смысле максимально отличающиеся друг от друга.

Лит.: Андерсон Т., Введение в многомерный статистический анализ, пер. с англ., М., 1963; Kendall М. G., Stuart А., The advanced theory of statistics, v. 3, L., 1966; Dempster A. P., Elements of continuons multivariate analysis, L., 1969.

А. В. Прохоров.

Статисти'ческий ана'лиз случа'йных проце'ссов,раздел математической статистики, посвященный методам обработки и использования статистических данных, касающихся случайных процессов (т. е. функций X ( t ) времени t , определяемых с помощью некоторого испытания и при разных испытаниях могущих в зависимости от случая принимать различные значения). Значение x ( t ) случайного процесса X ( t ), получаемое в ходе одного испытания, называется реализацией (иначе — наблюдённым значением, выборочным значением или траекторией) процесса X ( t ); статистические данные о X ( t ), используемые при статистическом анализе этого процесса, обычно представляютсобой сведения о значениях одной или нескольких реализаций x ( t ) в течение определенного промежутка времени или же о значениях каких-либо величин, связанных с процессом X ( t ) (например, о наблюденных значениях процесса Y ( t ), являющегося суммой X ( t ) и некоторого «шума» N ( t ), созданного внешними помехами и ошибками измерения значений x ( t )). Весьма важный с точки зрения приложений класс задач С. а. с. п. представляют собой задачи обнаружения сигнала на фоне шума, играющие большую роль при радиолокации. С математической точки зрения эти задачи сводятся к статистической проверке гипотез : здесь по наблюденным значениям некоторой функции требуется заключить, справедлива ли гипотеза о том, что функция эта является реализацией суммы шума N ( t ) и интересующего наблюдателя сигнала X ( t ), или же справедлива гипотеза о том, что она является реализацией одного лишь шума N ( t ). В случаях, когда форма сигнала X ( t ) не является полностью известной, задачи обнаружения часто включают в себя и задачи статистической оценки неизвестных параметров сигнала; так, например, в задачах радиолокации очень важна задача об оценке времени появления сигнала, определяющего расстояние до объекта, породившего этот сигнал. Задачи статистической оценки параметров возникают и тогда, когда по данным наблюдений за значениями процесса X ( t ) в течение определённого промежутка времени требуется оценить значения каких-то параметров распределения вероятностей случайных величин X ( t ) или же, например, оценить значение в фиксированный момент времени t = t 1 самого процесса Х ( t ) (в предположении, что t 1 лежит за пределами интервала наблюдений за этим процессом) или значение y ( t 1 ) какого-либо вспомогательного процесса Y ( t ), статистически связанного с Х ( t ) (см. Случайных процессов прогнозирование ). Наконец, ряд задач С. а. с. п. Относится к числу задач на непараметрические методы статистики; так обстоит дело, в частности, когда по наблюдениям за течением процесса X ( t ) требуется оценить некоторые функции, характеризующие распределения вероятностей значений этого процесса (например, плотность вероятности величины Х ( t ), или корреляционную функцию E x ( t ) X ( s ) процесса Х ( t ), или, в случае стационарного случайного процесса X ( t ), его спектральную плотность f ( l )