БСЭ БСЭ - Большая Советская Энциклопедия (СТ)

При решение задач С. а. с. п. всегда требуется принять те или иные специальные предположения о статистической структуре процесса X ( t ), т. е. как-то ограничить класс рассматриваемых случайных процессов. Очень ценным с точки зрения С. а. с. п. является допущение о том, что рассматриваемый процесс X ( t ) является стационарным случайным процессом; при этом допущении, зная значения единственной реализации x ( t ) в течение промежутка времени 0 £ t £ T , можно уже получить целый ряд статистических выводов о вероятностных характеристиках процесса X ( t ). В частности, среднеарифметическое значение

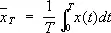
в случае стационарного случайного процесса X ( t ) при весьма широких условиях является состоятельной оценкой математического ожидания E x ( t ) = m (т. е. 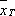сходится при Т ®¥ к истинному значению оцениваемой величины m ); аналогично этому выборочная корреляционная функция

,

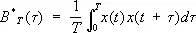где t > 0, при широких условиях является состоятельной оценкой корреляционной функции B (t) = E x ( t ) X ( t + t).

Однако Фурье преобразование функции 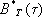— так называемая периодограмма I T (l) процесса X ( t ) — уже не представляет собой состоятельной оценки спектральной плотности f (l), являющейся преобразованием Фурье функции В (t); при больших значениях Т периодограмма I T (l) ведёт себя крайне нерегулярно и при Т ® ¥ она не стремится ни к какому пределу. Поэтому С. а. с. п. включает в себя ряд специальных приёмов построения состоятельных оценок спектральной плотности f (l) по наблюдённым значениям одной реализации стационарного процесса X ( t ), большинство из которых основано на использовании сглаживания периодограммы процесса по сравнительно узкой области частот l.

При исследовании статистических свойств оценок вероятностных характеристик стационарных случайных процессов очень полезными оказываются дополнительные допущения о природе X ( t ) (например, допущение о том, что все конечномерные распределения значений процесса X ( t ) являются нормальными распределениями вероятностей). Большое развитие получили также исследования по С. а. с. п., в которых предполагается, что изучаемый процесс X ( t ) является марковским процессом того или иного типа, или компонентой многомерного марковского процесса, или компонентой многомерного процесса, удовлетворяющего определённой системе стохастических дифференциальных уравнений.

Лит.: Дженкинс Г., Ватте Д., Спектральный анализ и его приложения, пер. с англ., в. 1—2, М., 1971—72; Хеннан Э., Анализ временных рядов, пер. с англ., М., 1964; его же, Многомерные временные ряды, пер. с англ., М., 1974: Липцер Р. Ш., Ширяев А. Н., Статистика случайных процессов (нелинейная фильтрация и смежные вопросы), М., 1974.

А. М. Яглом.

Статисти'ческий анса'мбль,совокупность сколь угодно большого числа одинаковых физических систем многих частиц («копий» данной системы), находящихся в одинаковых макроскопических состояниях; при этом микроскопические состояния системы могут принимать все возможные значения, совместимые с заданными значениями макроскопических параметров, определяющих её макроскопическое состояние. Примеры С. а. — энергетически изолированные системы при заданном значении полной энергии ( микроканонический ансамбль ), системы в контакте с термостатом заданной температуры ( канонический ансамбль ), системы в контакте с термостатом и резервуаром частиц (большой канонический ансамбль). С. а. — основное понятие статистической физики , позволяющее применить методы теории вероятностей.

Статисти'ческий вес,в квантовой механике и квантовой статистике — число различных квантовых состояний с данной энергией, т. е. кратность состояния. Если энергия принимает непрерывный ряд значений, под С. в. понимают число состояний в данном интервале энергий. В классической статистике С. в. называют величину элемента фазового объёма системы. См. Статистическая физика .

Статисти'ческий институ'тмеждународный, занимается развитием и усовершенствованием статистических методов и их применением в различных областях знаний. Основан в 1885. Организационная работа С. и. выполняется Постоянным бюро, которое находится в Гааге. В составе С. и. (середина 70-х гг.) свыше 700 действительных членов более чем из 70 стран (в т. ч. из СССР и др. социалистических стран), специалисты в области социально-экономической и математической статистики, а также руководители национальных статистических учреждений и организаций. Каждые 2 года С. и. проводит сессии, на которых заслушиваются и обсуждаются научные сообщения по проблемам различных отраслей статистики. Первая сессия состоялась в Риме в 1887, 40-я — в 1975 в Варшаве. Материалы сессий С. и. печатаются в «Бюллетенях института». Статьи по отдельным проблемам статистики (в основном математической) и текущая информация о научной жизни публикуются в журнале «Международное статистическое обозрение» («International statistical review», с 1933). До 1-й мировой войны 1914—18 С. и. был центром, международной статистики, занимался сбором и обработкой статистических данных отдельных стран, готовил рекомендации по сопоставимости данных. В 1919—33 он осуществлял эту деятельность параллельно с органами Лиги Наций . С созданием статистического аппарата ООН С. и. полностью переключился на вопросы статистической теории и методологии. Институт готовит кадры статистиков для развивающихся стран. В 70-е гг. сформировались 3 ассоциации как автономные секции С. и.: Международная ассоциация по применению статистики в физических науках, Международная ассоциация муниципальных статистиков, Международная ассоциация специалистов по выборочному методу.

Лит.: Рябушкин Т., Международная статистика, М., 1965.

Т. В. Рябушкин.

Статисти'ческий опера'тор,матрица плотности, оператор, с помощью которого можно вычислить среднее значение любой физической величины в квантовой статистической физике и, в частности, в квантовой механике . С. о. описывает состояние системы, не основанное на полном (в смысле квантовой механики) наборе данных о системе ( смесь состояний ).