БСЭ БСЭ - Большая Советская Энциклопедия (СТ)
- Название:Большая Советская Энциклопедия (СТ)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (СТ) краткое содержание
Большая Советская Энциклопедия (СТ) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Наиболее сложная задача метода группировок заключается в выделении и развёрнутой характеристике типов (т. н. типологическая С. г.) социально-экономических явлений, которые представляют собой выражение форм определенного общественного процесса, существенных особенностей, общих для многих единичных явлений. Ленин всесторонне, комплексно использовал метод группировок в своём анализе расслоения крестьянства, показав процесс формирования основных классов в дореволюционной России, в западно-европейской деревне и в сельском хозяйстве США.
Сов. статистика имеет большой опыт типологических С. г.: например, баланс народного хозяйства СССР предполагает сложную и разветвленную систему С. г.; группировка классового состава населения (табл. 2); группировка основных производственных фондов по социально-экономическим видам хозяйства; группировка совокупного общественного продукта и др.
В буржуазной статистике группировки используются недостаточно, а в случаях применения они большей частью строятся на неправильных основаниях, не способствуют характеристике действительного положения вещей в капиталистических странах, например группировка с.-х. предприятий по размерам земельной площади приукрашивает положение мелкого производства в сельском хозяйстве; группировка населения по занятиям не раскрывает действительную классовую структуру буржуазного общества и т.д.
Социально-экономические особенности социалистического общества ставят новые задачи перед С. г. Метод группировок применяется при анализе выполнения народно-хозяйственных планов, выяснении причин отставания отдельных предприятий и отраслей, выявлении неиспользованных резервов (например, С. г. предприятий по степени выполнения планов, степени рентабельности). С. г. предприятий по степени автоматизации и механизации, электровооружённости труда и по др. технико-экономическим признакам важны для характеристики внедрения достижений научно-технического прогресса в производство.
Табл. 1. — Группировка промышленных предприятий СССР по численности рабочих (1973, % к итогу)
| Группы предприятий | Число предприятий | Валовая продукция | Среднегодовая численность промышленно-производствен- ного персонала | Среднегодовая стоимость промышленно-производ- ственных основных фондов |
| Предприятия, состоящие на самостоятельном балансе (без электростанций, электросетей и теплосетей) | 100 | 100 | 100 | 100 |
| В том числе предприятия со среднегодовой численностью рабочих: | ||||
| до 100 | 35,0 | 4,2 | 3,4 | 2,9 |
| 101—200 | 19,6 | 5,9 | 5,5 | 4,0 |
| 201—500 | 22,9 | 14,0 | 13,9 | 11,2 |
| 501-1000 | 11,3 | 14,4 | 14,9 | 13,2 |
| 1001—3000 | 8,4 | 25,9 | 26,6 | 25,8 |
| 3001—10000 | 2,5 | 24,0 | 24,1 | 26,5 |
| 10001 и более | 0,3 | 11,6 | 11,6 | 16,4 |
Табл. 2. — Классовый состав населения СССР, %
| 1913 | 1928 | 1975 | |
| Всё население (включая неработающих членов семей) | 100 | 100 | 100 |
| В том числе: | |||
| Рабочие и служащие | 17,0 | 17,6 | 82,9 |
| из них рабочие | 14,6 | 12,4 | 60,9 |
| Колхозное крестьянство и кооперированные кустари | 2,9 | 17,1 | |
| Крестьяне-единоличники и некооперированные кустари | 66,7 | 74,9 | 0,0 |
| Буржуазия, помещики, торговцы и кулаки | 16,3 | 4,6 | — |
Лит . см. при ст. Статистика .
Т. В. Рябушкин.
Статистические оценки
Статисти'ческие оце'нки,функции от результатов наблюдений, употребляемые для статистического оценивания неизвестных параметров распределения вероятностей изучаемых случайных величин. Например, если X 1 ,..., X n — независимые случайные величины, имеющие одно и то же нормальное распределение с неизвестным средним значением а , то функции — среднее арифметическое результатов наблюдений
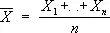
и выборочная медиана m = m( X 1,..., X n ) являются возможными точечными С. о. неизвестного параметра а . В качестве С. о. какого-либо параметра q естественно выбрать функцию q *( X 1,..., X n ) от результатов наблюдений X 1,..., X n , в некотором смысле близкую к истинному значению параметра. Принимая какую-либо меру «близости» С. о. к значению оцениваемого параметра, можно сравнивать различные оценки по качеству. Обычно мерой близости оценки к истинному значению параметра служит величина среднего значения квадрата ошибки
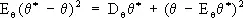
(выражающаяся через математическое ожидание оценки E 0q* и её дисперсию D 0q*). В классе всех несмещённых оценок (для которых E 0q* = 0) наилучшими с этой точки зрения будут оценки, имеющие при заданном n минимальную возможную дисперсию при всех q. Указанная выше оценка Х для параметра а нормального распределения является наилучшей несмещенной оценкой, поскольку дисперсия любой другой несмещенной оценки а* параметра а удовлетворяет неравенству 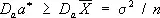 , где s 2 — дисперсия нормального распределения. Если существует несмещенная оценка с минимальной дисперсией, то можно найти и несмещенную наилучшую оценку в классе функций, зависящих только от достаточной статистики . Имея в виду построение С. о. для больших значений n , естественно предполагать, что вероятность отклонений q* от истинного значения параметра q, превосходящих какое-либо заданное число, будет близка к нулю при n ®¥. С. о. с таким свойством называются состоятельными оценками. Несмещенные оценки, дисперсия которых стремится к нулю при n ®¥, являются состоятельными. Поскольку скорость стремления к пределу играет при этом важную роль, то асимптотическое сравнение С. о. производят по отношению их асимптотической дисперсии. Так, среднее арифметическое Х в приведённом выше примере — наилучшая и, следовательно, асимптотически наилучщая оценка для параметра а , тогда как выборочная медиана m, представляющая собой также несмещенную оценку, не является асимптотически наилучшей, т.к.
, где s 2 — дисперсия нормального распределения. Если существует несмещенная оценка с минимальной дисперсией, то можно найти и несмещенную наилучшую оценку в классе функций, зависящих только от достаточной статистики . Имея в виду построение С. о. для больших значений n , естественно предполагать, что вероятность отклонений q* от истинного значения параметра q, превосходящих какое-либо заданное число, будет близка к нулю при n ®¥. С. о. с таким свойством называются состоятельными оценками. Несмещенные оценки, дисперсия которых стремится к нулю при n ®¥, являются состоятельными. Поскольку скорость стремления к пределу играет при этом важную роль, то асимптотическое сравнение С. о. производят по отношению их асимптотической дисперсии. Так, среднее арифметическое Х в приведённом выше примере — наилучшая и, следовательно, асимптотически наилучщая оценка для параметра а , тогда как выборочная медиана m, представляющая собой также несмещенную оценку, не является асимптотически наилучшей, т.к.
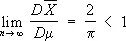
(тем не менее использование m имеет также положительные стороны: например, если истинное распределение не является в точности нормальным, а несколько отличается от него, дисперсия Х может резко возрасти, а дисперсия m остаётся почти той же, т. е. m обладает свойством, называется «прочностью»). Одним из распространённых общих методов получения С. о. является метод моментов, который заключается в приравнивании определённого числа выборочных моментов к соответствующим моментам теоретического распределения, которые суть функции от неизвестных параметров, и решении полученных уравнений относительно этих параметров. Хотя метод моментов удобен в практическом отношении, однако С. о., найденные при его использовании, вообще говоря, не являются асимптотически наилучшими, Более важным с теоретической точки зрения представляется максимального правдоподобия метод , который приводит к оценкам, при некоторых общих условиях асимптотически наилучшим. Частным случаем последнего является наименьших квадратов метод . Метод С. о. существенно дополняется оцениванием с помощью доверительных границ .
Читать дальшеИнтервал:
Закладка:
