БСЭ БСЭ - Большая Советская Энциклопедия (СТ)

Из этих формул видно, что относительные флуктуации объёма и флуктуации температуры обратно пропорциональны 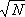, где N — число частиц в теле. Это и обеспечивает малость флуктуаций для макроскопических тел. Связь между флуктуациями различных величин x i , x k характеризуется функцией 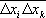. Если флуктуации величин x i и x k статистически независимы, то .

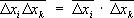Под x i и x k можно понимать и значения одной и той же величины, например плотности, в различных точках пространства. Тогда эта функция имеет смысл пространственной корреляционной функции. С увеличением расстояния между точками корреляционная функция стремится к нулю (обычно экспоненциально), т.к. флуктуации в далёких точках пространства происходят независимо. Расстояние, на котором эта функция существенно убывает, называется корреляционным радиусом.

Временной ход флуктуаций и спектральное распределение флуктуационного шума описываются временной корреляционной функцией j( t ), в которой усредняются флуктуации величины, взятые в различные моменты времени t :

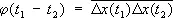
Важную роль в теории флуктуаций играет т. н. флуктуационно-диссипативная теорема, связывающая флуктуации в системе с изменением её свойств под влиянием определённых внешних воздействий. Простейшее соотношение такого рода можно получить, рассматривая флуктуации гармонического осциллятора с потенциальной энергией 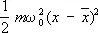, где m — масса осциллятора, w 0 — его собственная частота. Вычисление с помощью формулы (22) даёт: 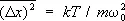. С др. стороны, если на осциллятор действует сила f , среднее значение 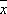смещается на величину 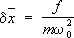, так что

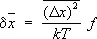(24)

и флуктуация х действительно связана с возмущением под влиянием силы f . В общем случае флуктуационно-диссипативная теорема применима, если для х существует «обобщённая сила» f , которая входит в оператор энергии системы (гамильтониан; см. Квантовая механика ) в виде члена 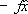, где 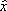— квантовомеханический оператор, соответствующий величине х . Включение силы f приведёт к изменению среднего значения 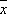на величину d 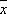, причём, если f зависит от времени как е -i wt, это изменение можно записать в виде:

;

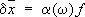комплексная величина a(w) называется обобщённой восприимчивостью системы. Теорема утверждает, что фурье-образ корреляционной функции

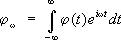
выражается через a следующим образом:

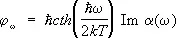(25)

(Im означает мнимую часть функции). Частным случаем (25) является Найквиста формула .

С. ф. неравновесных процессов.Всё большее значение приобретает кинетика физическая — раздел С. ф., изучающий процессы в системах, находящихся в неравновесных состояниях. Здесь возможны две постановки вопроса. Во-первых, можно рассматривать систему в некотором неравновесном состоянии и следить за её переходом в состояние равновесия. Во-вторых, можно рассматривать систему, неравновесное состояние которой поддерживается внешними условиями, например тело, в котором задан градиент температуры, протекает электрический ток и т.п., или тело, находящееся в переменном внешнем поле.

Если отклонение от равновесия мало, неравновесные свойства системы описываются т. н. кинетическими коэффициентами. Примерами таких коэффициентов являются коэффициенты вязкости , теплопроводности и диффузии , электропроводность металлов и т.п. Эти величины удовлетворяют принципу симметрии кинетических коэффициентов, выражающему симметрию уравнений механики относительно изменения знака времени (см. Онсагера теорема ). В силу этого принципа, например, электропроводность кристалла описывается симметричным тензором .

Описание сильно неравновесных состояний, а также вычисление кинетических коэффициентов производятся с помощью кинетического уравнения. Это уравнение представляет собой интегро-дифференциальное уравнение для одночастичной функции распределения (в квантовом случае — для одночастичной матрицы плотности, или статистического оператора ). Такое замкнутое, т. е. не содержащее др. величин, уравнение невозможно получить в общем виде. При его выводе необходимо использовать малые параметры, имеющиеся в данной конкретной задаче. Важнейшим примером является кинетическое уравнение Больцмана , описывающее установление равновесия в газе за счёт столкновений между молекулами. Оно справедливо для достаточно разреженных газов, когда длина свободного пробега велика по сравнению с расстояниями между молекулами. Конкретный вид этого уравнения зависит от эффективного сечения рассеяния молекул друг на друге. Если это сечение известно, уравнение можно решать, разлагая искомую функцию по ортогональным полиномам (см. Ортогональная система функций ). Таким способом можно вычислить кинетические коэффициенты газа, исходя из известных законов взаимодействия между молекулами. Уравнение Больцмана учитывает только парные столкновения между молекулами и описывает только первый неисчезающий член разложения этих коэффициентов по плотности газа. Удалось найти и более точное уравнение, учитывающее также тройные столкновения, что позволило вычислить следующий член разложения.

Особую проблему представляет вывод кинетического уравнения для плазмы. Из-за медленного убывания кулоновских сил с расстоянием даже при рассмотрении парных столкновений существенно экранирование этих сил остальными частицами.