БСЭ БСЭ - Большая Советская Энциклопедия (СТ)

Неидеальный газ.Важное достижение С. ф. — вычисление поправок к термодинамическим величинам газа, связанных с взаимодействием между его частицами. С этой точки зрения уравнение состояния идеального газа является первым членом разложения давления реального газа по степеням плотности числа частиц, поскольку всякий газ при достаточно малой плотности ведёт себя как идеальный. С повышением плотности начинают играть роль поправки к уравнению состояния, связанные с взаимодействием. Они приводят к появлению в выражении для давления членов с более высокими степенями плотности числа частиц, так что давление изображается т. н. вириальным рядом вида:

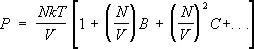. (15)

Коэффициенты В , С и т.д. зависят от температуры и наываются. вторым, третьим и т.д. вириальными коэффициентами. Методы С. ф. позволяют вычислить эти коэффициенты, если известен закон взаимодействия между молекулами газа. При этом коэффициенты В , С ,... описывают одновременное взаимодействие двух, трёх и большего числа молекул. Например, если газ одноатомный и потенциальная энергия взаимодействия его атомов U ( r ), то второй вириальный коэффициент равен

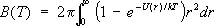. (16)

По порядку величины В равен 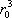, где r 0 — характерный размер атома, или, точнее, радиус действия межатомных сил. Это означает, что ряд (15) фактически представляет собой разложение по степеням безразмерного параметра Nr 3/V , малого для достаточно разреженного газа. Взаимодействие между атомами газа носит характер отталкивания на близких расстояниях и притяжения на далёких. Это приводит к тому, что В > 0 при высоких температурах и В < 0 при низких. Поэтому давление реального газа при высоких температурах больше давления идеального газа той же плотности, а при низких — меньше. Так, например, для гелия при Т = 15,3 К коэффициент В = — 3×10 -23 см 3 , а при T = 510 К В = 1,8 ×10 -23 см 3 . Для аргона В = — 7,1×10 -23 см 3 при Т = 180 К и В = 4,2×10 -23 см 3 при Т = 6000 К. Для одноатомных газов вычислены значения вириальных коэффициентов, включая пятый, что позволяет описывать поведение газов в достаточно широком интервале плотностей (см. также Газы ).

Плазма.Особый случай неидеального газа представляет собой плазма — частично или полностью ионизованный газ, в котором поэтому имеются свободные электроны и ионы. При достаточно малой плотности свойства плазмы близки к свойствам идеального газа. При вычислении же отклонений от идеальности существенно, что электроны и ионы взаимодействуют электростатически по закону Кулона. Кулоновские силы медленно убывают с расстоянием, и это приводит к тому, что уже для вычисления первой поправки к термодинамическим функциям необходимо учитывать взаимодействие не двух, а сразу большого количества частиц, поскольку интеграл во втором вириальном коэффициенте (16), описывающий парное взаимодействие, расходится на больших расстояниях r между частицами. В действительности под влиянием кулоновских сил распределение ионов и электронов в плазме изменяется таким образом, что поле каждой частицы экранируется, т. е. быстро убывает на некотором расстоянии, называемом дебаевским радиусом. Для простейшего случая плазмы, состоящей из электронов и однозарядных ионов, дебаевский радиус r D равен:

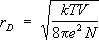, (17)

где N число электронов, е — заряд электрона. Все частицы, находящиеся внутри дебаевского радиуса, принимают участие во взаимодействии одновременно. Это приводит к тому, что первая поправка к давлению пропорциональна не ( N/V ) 2 как в обычном газе, а более низкой степени плотности — ( N/V ) 3/2 . Количественный расчёт основан на том, что остальные частицы распределены в поле выбранного электрона или иона согласно распределению Больцмана. В результате уравнение состояния с учётом первой поправки имеет вид:

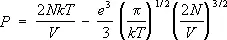(18)

(т.к. число электронов равно числу ионов, полное число частиц равно 2N ). Такого же рода поправки возникают и в термодинамических функциях электролитов, в которых имеются свободные ионы растворённых веществ.

Жидкости.В отличие от газа, связанные с взаимодействием члены в уравнении состояния жидкости не малы. Поэтому свойства жидкости сильно зависят от конкретного характера взаимодействия между её молекулами. В теории жидкости вообще отсутствует малый параметр, который можно было бы использовать для упрощения теории. Невозможно получить какие-либо аналитические формулы для термодинамических величин жидкости. Одним из способов преодоления этой трудности является изучение системы, состоящей из сравнительно небольшого числа частиц — порядка нескольких тысяч. В этом случае, используя ЭВМ, можно провести прямое решение уравнений движения частиц и определить таким способом средние значения всех характеризующих систему величин без дополнительных предположений. При этом можно исследовать также и процесс приближения такой системы к состоянию равновесия. Можно также найти статистический интеграл для такой системы из небольшого числа частиц путём вычисления на ЭВМ интегралов в основной формуле для статистического интеграла (обычно при этом используется Монте-Карло метод ). Полученные обоими способами результаты имеют, однако, малую точность в приложении к реальным жидкостям из-за малого числа частиц в системе.

Ещё один способ построения теории жидкости основан на использовании функций распределения молекул. Если проинтегрировать функцию распределения w системы по импульсам всех частиц и по координатам всех частиц, кроме одной, получится одночастичная пространственная функция распределения f 1 ( r ). Если проинтегрировать w по импульсам всех частиц и по координатам всех частиц, кроме двух, получится двухчастичная функция распределения f 2 ( r 1, r 2 ), всех частиц, кроме трёх, — трёхчастичная функция распределения f 3 ( r 1, r 2, r 3, ) и т.д. Двухчастичная функция распределения является непосредственно наблюдаемой физической величиной — через неё выражается, например, упругое рассеяние рентгеновских лучей и нейтронов в жидкости. Считая, что функция распределения всей системы даётся распределением Гиббса (6), можно получить интегральное соотношение, выражающее двухчастичную функцию через трёхчастичную и потенциал взаимодействия между частицами. В теории жидкости это точное соотношение дополняется некоторыми приближёнными, выражающими трёхчастичную функцию через двухчастичную (одночастичная функция в однородной жидкости сводится к постоянной). В результате получается уравнение для двухчастичной функции, которое решается численно. Дополнительные соотношения находятся на основании правдоподобных физических соображений и носят интерполяционный характер, так что основанные на них теории могут претендовать лишь на качественное описание свойств жидкости. Тем не менее даже такое качественное описание имеет важное значение, поскольку в нём проявляется общность законов С. ф. (см. также Жидкость ).