БСЭ БСЭ - Большая Советская Энциклопедия (СТ)

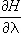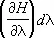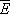Далее, пусть функция Гамильтона системы зависит от некоторого параметра l (координаты стенки сосуда, в который заключена система, внешнего поля и т.п.). Тогда производная будет обобщённой силой , соответствующей этому параметру, а величина после усреднения даёт механическую работу, совершаемую над системой при изменении этого параметра. Если продифференцировать выражение для средней энергии системы с учетом формулы (6) и условия нормировки, считая переменными l и T и учитывая, что величина F тоже является функцией от этих переменных, то получится тождество:

.

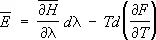Согласно сказанному выше, член, содержащий d l, равен средней работе dA , совершаемой над телом. Тогда последний член есть получаемое телом тепло. Сравнивая это выражение с соотношением dE = dA + TdS , представляющим собой объединённую запись первого и второго начал термодинамики (см. Второе начало термодинамики ) для обратимых процессов , находим, что T в (6) действительно равна абсолютной температуре тела, а производная 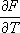— взятой с обратным знаком энтропии S . Это означает, что F есть свободная энергия тела, откуда выясняется её статистический смысл.

Особое значение имеет статистическое истолкование энтропии, которое следует из формулы (8). Формально суммирование g этой формуле производится по всем состояниям с энергией E n , но фактически ввиду малости флуктуаций энергии в распределении Гиббса существенно лишь относительно небольшое их число с энергией вблизи средней энергии. Число этих существенных состояний естественно определить поэтому, ограничив суммирование в (8) интервалом , заменив E n на среднюю энергию 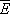и вынося экспоненту из-под знака суммы. Тогда сумма даст и примет вид.

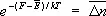
С др. стороны, согласно термодинамике, F = 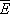— TS , что дает связь энтропии с числом микроскопических состояний в данном макроскопическом состоянии, иначе говоря, — со статистическим весом макроскопического состояния, т. е. с его вероятностью:

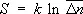. (10)

При температуре абсолютного нуля любая система находится в определённом основном состоянии, так что = 1, S = 0. Это утверждение выражает собой третье начало термодинамики . Здесь существенно, что для однозначного определения энтропии нужно пользоваться именно квантовой формулой (8); в чисто классической статистике энтропия определена только с точностью до произвольного слагаемого.

Смысл энтропии как меры вероятности состояния сохраняется и по отношению к произвольным — не обязательно равновесным — состояниям. В состоянии равновесия энтропия имеет максимальное возможное в данных внешних условиях значение. Это означает, что равновесное состояние является состоянием с максимальным статистическим весом, наиболее вероятным состоянием. Процесс перехода системы из неравновесного состояния в равновесное есть процесс перехода из менее вероятных состояний в более вероятные; это выясняет статистический смысл закона возрастания энтропии, согласно которому энтропия замкнутой системы может только увеличиваться.

Формула (8), связывающая свободную энергию F со статистической суммой, является основой для вычисления термодинамических величин методами С. ф. Она используется, в частности, для построения статистической теории электрических и магнитных свойств вещества. Например, для вычисления магнитного момента тела в магнитном поле следует вычислить статистическую сумму и свободную энергию. Магнитный момент m тела дается тогда формулой:

m = ,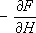

где Н — напряженность внешнего магнитного поля. Аналогично (8) условие нормировки в большом каноническом распределении (9) определяет термодинамический потенциал W согласно формуле:

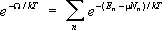. (11)

Этот потенциал связан со свободной энергией соотношением:

.

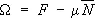Приложения С. ф. к изучению тех или иных свойств конкретных систем сводятся по существу к приближённому вычислению статистической суммы с учётом специфических свойств системы.

Во многих случаях эта задача упрощается применением закона равнораспределения по степеням свободы, утверждающего, что теплоёмкость c v (при постоянном объёме v ) системы взаимодействующих материальных точек — частиц, совершающих гармонические колебания, равна

c v= k ( l/2 + n ) ,

где l — общее число поступательных и вращательных степеней свободы, n — число колебательных степеней свободы. Доказательство закона основано на том, что функция Гамильтона Н такой системы имеет вид: Н = K ( p i ) + U ( q m ), где кинетическая энергия К — однородная квадратичная функция от l + n импульсов p i а потенциальная энергия U — квадратичная функция от n колебательных координат q m . В статистическом интеграле Z (8а) интегрирование по колебательным координатам ввиду быстрой сходимости интеграла можно распространить от - ¥ до ¥. Сделав после этого замену переменных 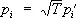, 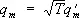находим, что Z зависит от температуры как T l/2+n , так что свободная энергия F = — kT ( l/ 2 + n )(ln T + const). Отсюда следует приведённое выше выражение для теплоёмкости, поскольку 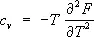. Отклонения от закона равнораспределения в реальных системах связаны прежде всего с квантовыми поправками, т.к. в квантовой С. ф. этот закон несправедлив. Существуют также поправки, связанные с негармоничностью колебаний.